איך פותרים מערכת של משוואות לינאריות בעזרת מטריצה?
אנו ניקח את מערכת המשוואות הנתונה שצריך לפתור, ונוציא ממנה את המטריצה המורחבת M .
עכשיו נעבוד עם המטריצה המורחבת M , כלומר נצמצם את שורותיה של המטריצה המורחבת של המערכת לצורה מדורגת ואז נצמצם אותה לצורה קנונית אשר מובילה לפתרון.
ההצדקה לתהליך זה נובעת מהעובדות הבאות:
א) כל פעולת שורה אלמנטרית על המטריצה המורחבת M של המערכת, שקולה ליישום הפעולה המתאימה על המערכת עצמה. ב) למערכת יש פתרון אם ורק אם בצורה המדורגת של המטריצה Mאין שורה מהצורה (0.0,0...,0,b) עם b ששונה מאפס. ג) בצורתה הקנונית של המטריצה M (לאחר שהוצאו ממנה שורות אפסים) המקדם של כל משתנה שאינו חופשי הוא איבר מוביל השונה מאפס , כלומר שווה ל-1, והוא האיבר השונה מאפס היחיד בעמודתו. על כן הפתרון הכללי מושג בפשטות ע"י חילוץ המשתנים הלא- חופשיים.
מסובך? נביא כעת מספר דוגמאות אשר יבהירו את תהליך זה.
דוגמאות
א) פתור את המערכת:
x + y - 2z + 4t = 5
2x + 2y - 3z + t = 4
3x +3y - 4z - 2t = 1
את המערכת הזו נפתור ע"י צמצום המטריצה המורחבת M לצורה מדורגת ואח"כ לקנונית, כלהלן:
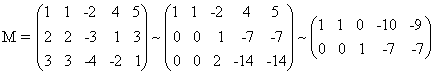
השורה השלישית במטריצה השנייה נמחקה, מאחר שהיא כפולה של השורה השנייה, ולכן תיתן שורת אפסים.
על- כן צורת הפתרון הכללי של המערכת היא זו:
x + y - 10t = -9 או x = -9 - y +10t
z - 7t = -7 z = -7 + 7t
כאן המשתנים החופשים הם y ו- t, והמשתנים הלא חופשים הם x ו- z.
ב)
נפתור את המערכת :
x1 + x2 - 2x3 + 3x4 = 4
x1 + 3x2 + 3x3 - x4 = 32
5x1 + 7x2 + 4x3 + x4 = 5
ע"י צמצום המטריצה המורחבת למדורגת:
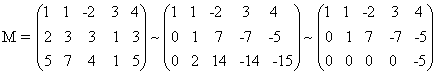
אין צורך להמשיך ולמצוא את הצורה הקנונית של המטריצה מאחר שהמטריצה המדורגת כבר מעידה על כך שלמערכת אין פתרון, כי השורה השלישית של המטריצה המדורגת מתאימה למשוואה :
0x1 + 0x2 + 0x3 + 0x4 = -5
שאין לה פתרון.
ג) המערכת
X + 2y + z = 3
2x + 5y - z = -4
3x - 2y - z = 5
נפתרת ע"י צמצום המטריצה המורחבת M למדורגת ואז לקנונית:
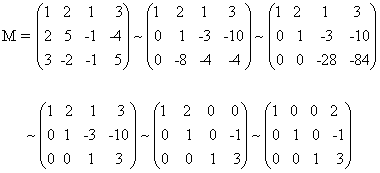
על – כן יש למערכת פתרון יחיד x = 2, y = -1, z = 3 או u = (2, -1, 3).
הצורה המדורגת של M העידה על כך שהפתרון הוא יחיד, שכן היא התאימה למערכת משולשת.
