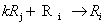שקילות שורה ופעולות שורה יסודיות
על מטריצה A נאמר שהיא שקולת שורות למטריצה B , אם ניתן לקבל את B מ- A ע"י סדרה סופית של הפעולות הבאות הנקראות פעולות שורה אלמנטריות(יסודיות):
| E1 : החלפת השורה ה- i והשורה ה - j - |
| E2: הכפלת השורה ה- i בסקלר שונה מאפס - |
|
E3 : החלפת השורה ה- i ב- k פעמים השורה ה- j ועוד השורה ה- i - |
יש דמיון בין פעולות אלו לאלו המשמשות בפתרון מערכות של משוואות לינאריות.
מסובך? אל דאגה! ניישם פעולות אלו ע"י הפיכת מטריצה לצורה מדורגת או צורה קנונית.
דוגמאות
א) נביא את המטריצה 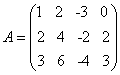 לצורה מדורגת:
לצורה מדורגת:
a11 = 1 השתמש ב-
כציר כדי לאפס את כל האיברים מתחת לאיבר זה, כלומר יישם את פעולות השורה:
![]() וקבל את המטריצה:
וקבל את המטריצה:
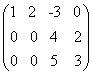
![]() וקבל את המטריצה:
וקבל את המטריצה:
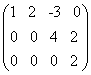
כעת המטריצה מדורגת.
ב) נביא את המטריצה המדורגת 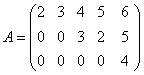 לצורה קנונית:
לצורה קנונית:
נכפיל את R3 ב- ¼ כך שהאיבר המוביל השונה מאפס יהיה שווה ל-1, ואז נשתמש
ב- a35 = 1 כציר כדי לאפס את האיברים שמעליו ע"י הפעולות:
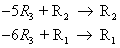
ונקבל:
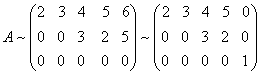
נכפיל כעת את R2 ב- 1/3 כך שהאיבר המוביל השונה מאפס שווה ל-1, ואז נשתמש
ב- a23 = 1 כציר כדי לאפס את האיבר שמעליו ע"י הפעולה:
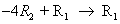
ונקבל:
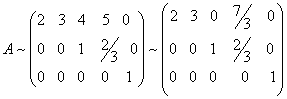
לבסוף, נכפיל את R1 ב- ½ ונקבל:
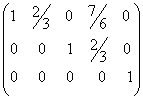
וזו המטריצה הקנונית של A.
כל מטריצה שקולת שורות למטריצה קנונית אחת ויחידה שנקראת הצורה הקנונית של A