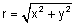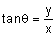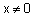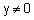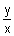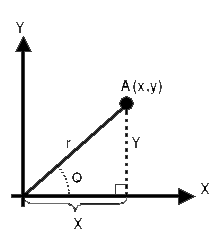
מעבר מתצוגה קרטזית לקוטבית:   בהנתן הנקודה (A(x,y מתקיים עפ"י משפט פיתגורס. ו עבור כאשר x = 0 ו- הביטוי לא מוגדר.
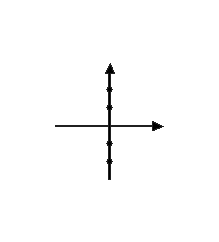
ולכן נעשה הבחנה בין הנקודות שנמצאות בחלק החיובי של ציר ה-y ובין אלו הנמצאות בחלק השלילי שלו. עבור y>0 נקבל ש- Q = 90 ועבור y<0 נקבל ש- Q = 270.

מעבר מתצוגה קוטבית לקרטזית:

בהנתן ההצגה הקוטבית (r,Q) של הנקודה (A(x,y השונה מ- (0,0) (לנקודה (0,0) אין הצגה קוטבית כיוון שקשה ליחס לה זווית). מתקיים:

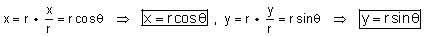
מכאן שההצגה הקוטבית של מספר מרוכב היא:

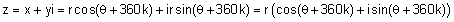
סימון: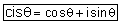