תהי(A(x,y הנקודה במישור גאוס המייצגת את המספר z = x+yi. ניתן להציג נקודה זו באמצעות הזוג(r, Q) כאשר r - מייצג את מרחק נקודה A מראשית הצירים ו- Q מייצג את הזווית הנוצרת בין הקטע AO לכיוון החיובי של ציר ה- X.
| כאשר Q אינה נקבעת באופן יחיד אלא עד כדי כפולה של | 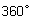 |
או בראדיאנים | 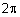 |
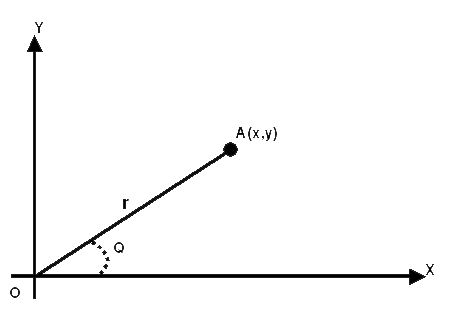
הערך המוחלט של מספר מרוכב הוא המרחק r מהראשית של המספר z = x+yi.
| והוא מסומן כך: | 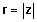 |
הארגומנט של מספר מרוכב הוא הזווית Q של המספר המרוכב z = x+yi.
והיא מסומנת כך: (Q = arg(z

