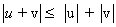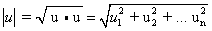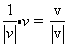נורמה של וקטור
יהא u = (u1, u2, ... un ) וקטור ב- Rn , הנורמה (או האורך) של הוקטור u,
|
|
מאחר ש- u ∙ v ≥ 0 השורש הריבועי קיים . בנוסף לכך, אם u ≠ 0
אז 0 < |u| .
כמו כן 0 = |0|
מסובך? הדוגמא הבאה תמחיש כיצד מוצאים נורמה של וקטור.
דוגמא
169 = 16 + 144 + 9 = 2 ( 4-) + 2 (12- ) + 32 = 2 |u|
אז |u| = √169 = 13
לוקטור שאורכו 1 נקרא וקטור מנורמל או וקטור יחידה.
כלומר אם |v| = 1 או לחילופין v ∙ v= 1 אז v וקטור היחידה.
לכל וקטור v שאינו וקטור האפס הוקטור :
|
|
הוא וקטור יחידה בכיוון של v .
התהליך של מציאת וקטור היחידה נקרא נרמול של v.
דוגמא
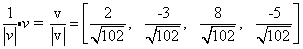
שהרי |v| = √102 בדוק!
כלומר וקטור זה הוא וקטור היחידה בכיון של הוקטור (5-, 8, 3- , 2 ) = u
כעת נציג קשר יסודי הידוע בשם אי- השויון של קושי- שוורץ
אי- השויון של קושי- שוורץ
לכל וקטורים שהם u, v ב- Rn מתקיים:
|
|
אי-השויון של מינקובסקי
לוקטורים כלשהם u , v ב- Rn :
גולשים מקוונים: 1