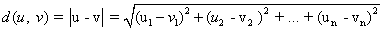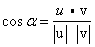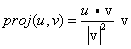מרחק, זויות והיטלים
יהיו v = (v1, v2, ...vn) ו- u= (u1, u2, ...un) וקטורים ב- Rn .
המרחק בין u ו- v שנסמנו ב- d(u, v) מוגדר כ:
|
|
נראה כי הגדרה זו מתאימה למושג הרגיל של מרחק אויקלידי במישור R2 :
נניח u = (a, b) ו- v = (c,d) ב- R2.
אם נצייר את הנקודות הללו במערכת צירים נגלה שהמרחק ביניהם (עפ"י משפט פיתגורס) הוא:
בדוק!
מצד שני באמצעות ההגדרה שלעיל,
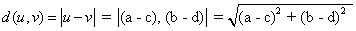
שניהם נותנים אותו ערך.
ע"י אי-השויון של קושי – שוורץ, נוכל להגדיר את הזוית α בין כל שני וקטורים שונים
מאפס u, v ב- Rn
|
|
שאם u ∙ v = 0, אזי 90 = α , כלומר שני הוקטורים ניצבים כלומר אורתוגונליים.
דוגמא
נניח ש- u = ( 1, -2, 3) ו- v = ( 3, -5, -7) אזי:
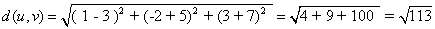
עכשיו נמצא את .cos α
כאשר α היא הזוית בין u ו- v , עלינו ראשית למצוא:
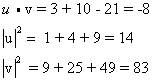
אזי:
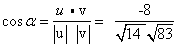
יהיו u ו- v וקטורים שונים מאפס ב- Rn .
וקטור ההיטל של u על v הוא הוקטור:
|
|
דוגמא
נניח ש- (3, 2-, 1) = u ו- ( 4, 5, 2) = v כדי למצוא את ( proj(u, v נמצא ראשית
u ∙ v = 2 - 10 + 12 = 4
45 = 16 + 25 + 4 = 2 |v|
ואז:
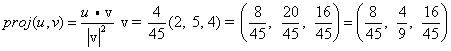
היטל הוא וקטור!
גולשים מקוונים: 3