מטריצות הפיכות(לא סינגולריות)
מטריצה ריבועית A נקראת הפיכה (או לא-סינגולרית) אם קיימת מטריצה B כך ש:
|
AB = BA = I |
כאשר I היא מטריצת היחידה.
מטריצה B כזו היא יחידה קל להוכיח זאת.
הוכחה: נניח שקימות שתי מטריצות AB1 = B1A = I ו- AB2 = B2A = I נובע מכך ש:
B1 = B1I = B1(AB2) =( B1A)B2 = IB2 = B2
כלומר B1 = B2 אותה המטריצה ולכן יחידה.
למטריצה B קוראים ההופכית של A ומסמנים אותה ב- A-1
היחס הזה הוא סימטרי , כלומר אם B ההופכית של A , אזי A היא ההופכית של B
דוגמאות
א) נניח ![]() אזי:
אזי:
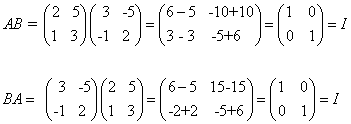
על כן A ו- B הפיכות והן הופכיות זו לזו.
ב) נשאיר לכם לבדוק שהמטריצות:
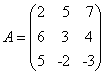 ו-
ו- 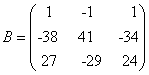 הן אחת ההופכית של השניה כלומר
הן אחת ההופכית של השניה כלומר
AB=BA=I
ג) בדוגמא זו נראה כיצד בודקים שמטריצה אינה הפיכה.
נראה שהמטריצה ![]()
נניח בשלילה שהמטריצה 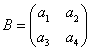 הופכית של A
הופכית של A
כלומר צריך להתקיים השוויון 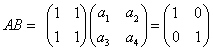
את השוויון הנ"ל נרשום כמערכת משוואות 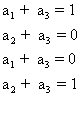
למערכת הנ"ל אין פתרון, לכן ל- A אין מטריצה הופכית.
תכונות של מטריצות הפיכות
תהיינה A ו- B מטריצות הפיכות , אזי:
א) At הפיכה ומתקיים At) -1= (A-1) t)
ב) AB הפיכה ומתקיים B-1A-1 = 1-(AB)
