המשך פתרון תרגיל מס' 3
פתרון שאלה מס' 11
הראה כיצד הבסיס נותן את הצורה הפר מטרית של הפתרון הכללי של המערכת:
הבא לצורה מדורגת. הפעל: 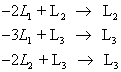
וקבל:
x + 2y - 2z + 5s - 3t = 0 x + 3y - 2z + 5s - 3t = 0
Y + z - 3s + t = 0 ו- y + z - 3s + t = 0
2y + 2z - 5s = 0 s - 2t = 0
בצורה המדורגת, יש למערכת שני משתנים חופשים z ו- t לכן dim = 2 .
בסיס (u1, u2) ל- w ניתן לקבל כך:
1) הצב z = 1 , t = 0, הצבה לאחור נותנת s = 0, y = -1, x = 5
על- כן u1 = (5, -1, 1, 0, 0)
2) הצב z = 0, t = 1, הצבה לאחור נותנת s = 2, y = 5, x = -22
על – כן u2 = (-22, 5, 0, 2, 1)
הכפלת וקטורי הבסיס בפרמטרים a ו- b בהתאמה נותנת:
Au1 + bu2 = a(5, -1, 1, 0, 0) + b (-22, 5, 0, 2, 1) =
( 5a - 22b, -a + 5b, a, 2b, b)
זו הצורה הפר מטרית של הפתרון הכללי.
פתרון שאלה מס' 12
הבא את המערכת לצורה מדורגת וקבל:
x + 2y - 3z = 0
Y + 8z = 0
61z = 0
אין משתנים חופשים – המערכת היא בצורה משולשת , על – כן dim W = 0
ול- W אין בסיס. כלומר W מורכב רק מפתרון האפס W = {0}.
פתרון שאלה מס' 14
ראשית רשום כל צד כמטריצה בודדת:
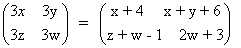
השווה איברים מתאימים וקבל את מערכת ארבע המשוואות
3x = x + 4 2x = 4
3y = x + y + 6 או 2y = 6 + x
3z = z + w – 1 2z = w -1
3w = 2w + 3 w = 3
הפתרון הוא: x = 2, y= 4, z= 1, w = 3.
פתרון שאלה מס' 15
א) מאחר ש- A היא 2 X 2 , ו- B היא 2 X 3 , המכפלה AB מוגדרת והיא מטריצה 2 X 3 כדי לקבל את רכיבי השורה הראשונה של AB, כפול את השורה הראשונה (1,3) של A בעמודות: ![]() של B בהתאמה:
של B בהתאמה:
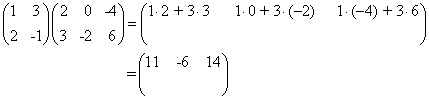
כדי לקבל את רכיבי השורה השניה של AB , כפול את השורה השניה (1-, 2)
של A בעמודות של B בהתאמה.
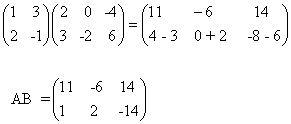
ב) שים לב ש- B היא 2 x 3 ו- A היא 2 x 2 מאחר שהמספרים הפנימיים 3 ו- 2 אינם שווים , המכפלה BA אינה מוגדרת.
פתרון שאלה מס' 17
כתוב מחדש את שורות A כעמודות וקבל את AT , ואז כתוב מחדש את שורות AT כעמודות, וקבל את T (AT):
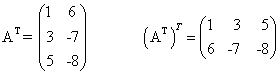
כפי שצפוי כי הרי A =T (AT)
פתרון שאלה מס' 18
אם A היא מטריצה כללית m x n, אזי AT היא מטריצה n x m, על-כן, AAT מוגדרת כמטריצה m x m ו- ATA מוגדרת כמטריצה n x n.
