גרפים של מהירות ומיקום

 

נשרטט גרף לדוגמה, המתאר תנועה לאורך זמן:

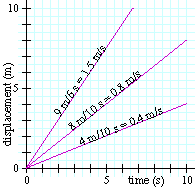
כל אחד משלושת הקווים מתאר תנועה שונה. מצד שמאל אנו רואים את המיקום, ולמטה נמצא ציר הזמן. הקווים אומרים מהו מיקומו של כל אחד משלושת הגופים המתוארים, בכל זמן שהוא.

 

• כיצד אפשר ללמוד על המהירות מתוך גרף המיקום?

אמרנו כבר כי כדי לדעת את המהירות, אנחנו צריכים לקחת שני מיקומים, לומר שהמרחק שביניהם הוא xD, ושפער הזמן (בין הזמן בו הגוף היה במיקום אחד לבין הזמן בו היה במיקום השני) הוא tD, ואז לחשב .

אם פער הזמן קטן מספיק, לפנינו מהירות נקודתית מדוייקת, ואם לא אז זו רק מהירות ממוצעת.

 

את כל החישובים הללו ניתן לבצע על הגרף!

ניתן לבחור שתי נקודות על הגרף. xD יהיה המרחק האנכי ביניהן, ו- tD יהיה המרחק האופקי ביניהן. נוצר משולש ישר זווית שאחת מצלעותיו הניצבות מקבילה לציר הזמן ואילו השניה מקבילה לציר המיקום. היתר של המשולש היא הקו המחבר בין שתי הנקודות. כשנחלק את המרחק האנכי במרחק האופקי, נקבל את המהירות הממוצעת בין שתי הנקודות.

 

כאשר שתי הנקודות מאד קרובות זו לזו מתגלים שני דברים:

• המהירות המחושבת מהגרף אינה רק המהירות הממוצעת אלא המהירות הנקודתית.
• דבר מעניין נוסף שמתגלה, הוא שככל שנקרב את שתי הנקודות שבחרנו זו לזו, היתר של המשולש ילך ויעשה המשיק לגרף המיקום, כלומר, השיפוע שלו בנקודת האמצע בין שתי הנקודות.

 

מכאן אנו מגיעים למסקנה חשובה:

השיפוע של גרף המיקום בנקודה מסויימת עליו (שמורה על זמן מסויים), מלמד אותנו על המהירות באותה נקודה.

 

כאשר השיפוע תלול המהירות גבוהה, כאשר השיפוע מתון, המהירות קטנה, וכאשר גרף המיקום הוא קו אופקי, המהירות היא אפס.

כמו כן, בנקודות מינימום ומקסימום על גרף המיקום, בהם המשיק הוא קו אופקי, המהירות היא ג"כ אפס.

 

נסתכל שוב על הגרף שלמעלה, וננסה להבין מהי המהירות של הגופים המתוארים בו.ניתן לראות בקלות שהשיפוע של הקווים קבוע. הם קווים ישרים. מכאן נובע שהמהירות של הגופים קבועה.

 

נקח לדוגמה עוד גרף של מיקום מול זמן:

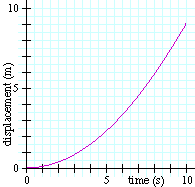
אפשר לראות איך השיפוע נעשה יותר ויותר תלול. זה אומר שהמהירות הולכת וגדלה.

כבר הזכרנו קודם שייתכן לדבר על מיקום שלילי. עכשיו אנו יכולים לראות שניתן גם לדבר על מהירות שלילית. בתנועה לאורך ציר מסויים, מהירות חיובית היא מהירות שמגמתה לכיוון החיובי של הציר, ומהירות שלילית היא כזו שמגמתה לכיוון השלילי של הציר.

 

ניתן לראות זאת גם דרך השיפוע- כאשר קו המיקום משתפל ויורד עם הזמן, זהו שיפוע שלילי, המורה על מהירות שלילית. ככל שהירידה יותר תלולה, מדובר על מהירות גדולה יותר לכיוון השלילי.

 

נסתכל על הגרף הבא:

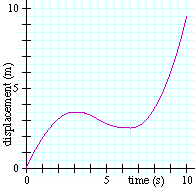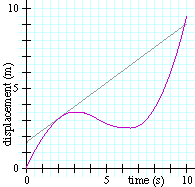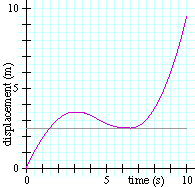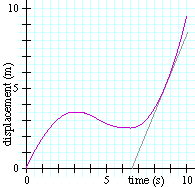
נעבור על מה שקורה משמאל (זמן אפס) ימינה-

התנועה מתחילה עם שיפוע גדול בעלייה (מהירות גדולה וחיובית) שהולך ומתמתן, כלומר, המהירות קטֵנה.

בנקודת המקסימום (בפסגה) אין שיפוע (המשיק אופקי), ולכן המהירות היא אפס.

כאן מתחיל להתפתח שיפוע של מדרון כלפי מטה, כלומר מהירות שלילית, עד לנקודת המינימום, בה שוב המהירות שווה אפס. משם מתפתח שיפוע חיובי עם מתלול גדל והולך, המראה על מהירות חיובית מתגברת.

 

ראינו כיצד ניתן ללמוד על המהירות מתוך גרף המיקום. עכשיו נראה כיצד ניתן ללמוד על המיקום מתוך גרף המהירות.נסתכל על גרף של מהירות (לא מיקום!) לאורך זמן:

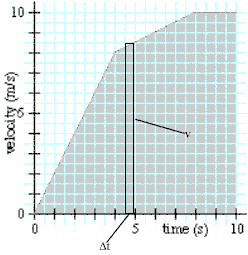
בחרנו שתי נקודות זמן קרובות, ושרטטנו בכל אחת מהן קו אנכי החותך את הגרף ואת ציר הזמן. בערך בגובה של הגרף בין שני הקוים האנכיים, ציירנו קו קטן אופקי וקיבלנו מלבן צר.

רוחבו של המלבן הוא פער הזמן בין שתי נקודות הזמן שבחרנו, נקרא לו tD. גובהו של המלבן הוא פחות או יותר ערך הגרף בין שתי נקודות הזמן, זוהי המהירות הממוצעת של הגוף בין שתי נקודות הזמן.

עכשיו ניתן לדעת מה המרחק שעבר הגוף בפער הזמן - כדי לקבל מרחק יש להכפיל את מהירות התנועה בזמן התנועה, כלומר

 x = v×Dt

בעצם זהו שטח המלבן (גובה כפול רוחב).

כמו שניתן לדעת כך את הדרך שנעשתה בין שתי נקודות, כך ניתן לדעת את הדרך הכללית, וזאת אם נצייר הרבה מלבנים צרים וצפופים ונחבר את שטחיהם.

בעצם, סכום שטחי המלבנים (אם הם מספיק צרים), הוא סך כל השטח שמתחת לגרף.

 

מכאן אנו מגיעים למסקנה:

השטח הכלוא בין גרף המהירות לציר הזמן בין שתי נקודות זמן, הוא המרחק שנעשה בין שתי נקודות אלה.

 

חשוב לזכור:

אם השטח הוא מתחת לציר הזמן, הוא מייצג מיקום שלילי!

 

נסתכל בסרטון המראה דוגמה של כל מה שלמדנו על גרפים עד כה.