באופן כללי ניתן לאשר נכונותן של טענות בעזרת אקסיומה הנקראת אקסיומת האינדוקציה המתמטית (השלמה):
|
טענה המתייחסת למספר טיבעי n נכונה לכל n אם היא מקיימת את התנאים הבאים:
(1) הטענה נכונה עבור 1=n
(2) מההנחה שהטענה נכונה עבור n=k , כאשר k מספר טיבעי, נובע שהיא נכונה עבור n=k+1 .
|
הרעיון הכללי: בודקים את נכונות הטענה עבור n=1 ע"י שמציבים 1 במקום n . ואז עפ"י שלב (2) הטענה נכונה עבור n=2 , שוב עפ"י שלב (2) הטענה נכונה עבור n=3 וכן הלאה.
בצורה זו נקבל שהטענה נכונה עבור כל המס' הטבעיים.
שלבים בהוכחה:
שלב א': בודקים את נכונות הטענה עבור n=1 ע"י הצבת 1 במקום n .
שלב ב': מניחים שהטענה נכונה עבור n=k , כאשר k הוא מס' טיבעי כלשהו. מציבים k במקום n.
שלב ג': זהו השלב בו רושמים את מה שצריך להוכיח , כלומר מציבים את n במקום את k+1 .
שלב ד': על סמך ההנחה בשלב ב' מוכיחים שהטענה מתקיימת עבור n=k+1 .
| הערה: ניתן להסתמך על האינדוקציה גם על מנת להוכיח שהטענה נכונה עבור | 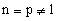 |
כלומר, 1<p.
לדוג': נכונות עבור מס' זוגיים ואי זוגיים.

