פתרון AX = B בעזרת ההופכית של A
נתון שמטריצות A, X , B מקימות AX = B .
כאשר A ו- B מטריצות נתונות, אם A מטריצה הפיכה ניתן למצוא את מטריצה X שהיא יחידה המקיימת את המשוואה באופן הבא:
נכפול את שני האגפים ב- A-1 , ונקבל:
|
AX = B / A-1 A-1 A X = A-1 B X = A-1B |
כלומר כדי למצוא את מטריצה X צריך למצוא את ההופכית של A (תוך שימוש באחת השיטות שלמדנו) ולכפול אותה במטריצה B.
קימת שיטה נוספת יותר פשוטה למציאת מטריצה B החוסכת את מציאת A-1 .
נעמיד את מטריצות A ו- B באופן הבא : ( A | B) ונבצע פעולות אלמנטריות על A ו- B באותו הסדר כך ש-A תהפוך תחת הפעולות למטריצה היחידה ו- B תהפוך למטריצה X .
שיטה זו מזכירה את התהליך של מציאת מטריצה הופכית.
דוגמאות
א) נתונות המטריצות הריבועיות :
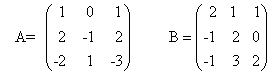
מצא את מטריצה X שמקיימת AX = B .
אנו נפתור בשיטה הפשוטה יותר.
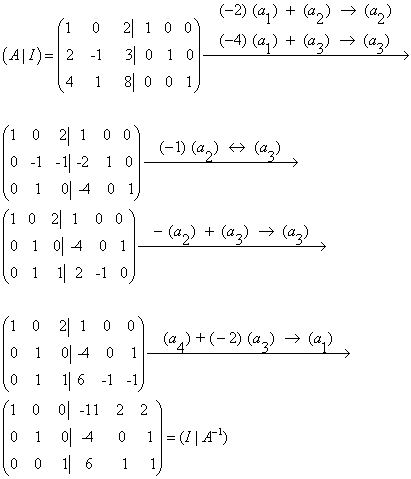
אם בתהליך הדירוג נוצר מצב של משתנה חופשי כלומר עמודה ללא איבר מוביל סימן ש- A לא הפיכה ולא ניתן להמשיך- לא קימת מטריצה X.
ב) פתור את מערכת המשואות Ax = bi
כאשר :
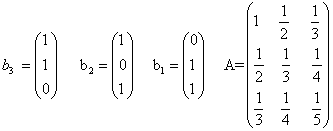
אפשר לפתור את שלוש המערכות של המשוואות זו אחר זו, אך ניתן גם לפתור אותן יחד.
נכפיל את שני האגפים של המשוואה ב- A-1 נקבל x = A-1bi .
כלומר אם נחשב את A-1 נקבל את שלושת הפתרונות.
נשאיר לכם לבדוק ש-
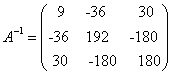
ונקבל ש-
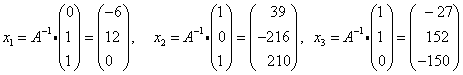
הידעת? מטריצה A שאיבריה
(כמו בדוג' הקודמת) נקראת מטריצת הילברט(Hilbert)
אם A היא מטריצת הילברט, אזי האיברים של A-1 הם מספרים שלמים.
גולשים מקוונים: 4