|
ההתפלגות הפואסונית משמשת קירוב טוב להתפלגות הבינומית כאשר מספר הניסוים המבוצעים (n) הוא גדול מאוד, וההסתברות ל"הצלחה" בכל ניסוי p , קרובה ל-0. אולם, להתפלגות זו חשיבות לכשלעצמה. כללית היא מתארת את ההסתברות כי אירוע מסויים יקרה k פעמים בזמן נתון t כאשר האירוע קורה באופן אקראי לחלוטין, וקיימת אי-תלות בין ההופעות השונות של האירוע.
לדוגמא:
1. מה ההסתברות כי בקטע כביש מסויים יעברו 10 מכוניות (k=10) בזמן של 5 שניות (t=5).
2. מה ההסתברות כי למרכזיית טלפונים יגיעו 25 שיחות (k=25) במשך 3 דקות ((t=3.
3. מה ההסתברות כי למחסן הטכני במפעל יגיעו בפרק זמן של שעה (t=1) שבעה עובדים (k=7) להוצאת ציוד.
|
|
יהי x משתנה מקרי בדיד היכול לקבל את הערכים x=0,1,2…
תהיה
x הינו משתנה מקרי פואסוני , אזי פונקצית ההסתברות שלו היא:
|
|
|
|
כאשר:
e = 2.718… (הבסיס של הלוגריתם הטבעי)
ציור של התפלגות פואסון
|
|
נהג מונית ממתין להופעת נוסעים (הוא נוסע רק כשהמונית מתמלאת). מנסיון העבר הוא יודע כי בממוצע מגיע נוסע אחד כל שתי דקות. בהנחה כי הנוסעים אינם מופיעים בקבוצות, מהי ההסתברות כי יוכל לצאת לדרך לאחר 5 דקות המתנה. (במוניתו מקום ל-7 נוסעים).
קצב מופע הנוסעים : 0.5 נוסעים לדקה =
5 דקותt =
k = 7
|
|
|
|
 |
||
 |
|
||
|
יום שישי 22 בנובמבר 2024
|
|
|
||||||||||||||||||||||||||||||||||||
 גולשים מקוונים: 4 |
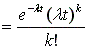(יתרחשו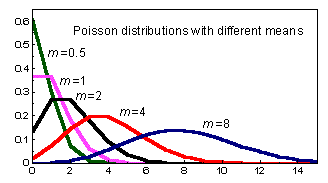 
.
.
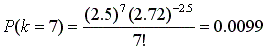דהיינו כאחוז אחד.
