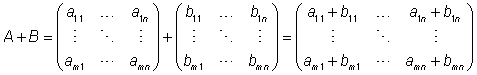פעולות חשבון במטריצות
בנושא זה נתחיל בפעולות הפשוטות יחסית שהם כפל בסקלר וחיבור וחיסור מטריצות ולאחר מכן נלמד כפל מטריצות שזוהי פפעולה מסובכת במידה מסוימת.
כפל במספר
לכל מטריצה Amxn מעל שדה F ומספר b מתוך F, נחשב את המטריצה
b*Aבאופן הבא:
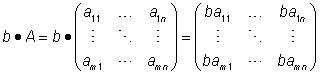
חיבור מטריצות
נגדיר את סכומן באופן הבא:
|
|
ש- A+B ו- kA גם הן מטריצות m x שסכום מטריצות בעלות גדלים שונים אינו מוגדר.
נגדיר: ( A = -1 * A A - B = A + (-B -
נביא דוגמא שתסביר את הפעולות הנ"ל.
דוגמא
תהיינה ![]() ן-
ן- ![]() אזי:
אזי:
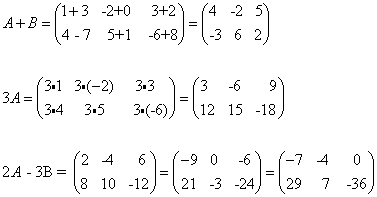
לפני שנגדיר כפל מטריצות שזו פעולה יותר מסובכת נביא תכונות בסיסיות של מטריצות תחת הפעולות של חיבור מטריצות וכפל בסקלר ותכונות של מטריצה משוחלפת
תכונות של מטריצות
לכל שלוש מטריצות מאותו הסדר C,B,A מעל F ו- מספרים a,b ב- F מתקיימות התכונות הבאות:
1. A + B = B + A
2. (A + B) + C = A + (B + C)
A + 0 = A .3
4. A + (-A) = 0
5. a (A + B) = aA +aB
6. (a + b) A = aA + bA
7. (a b) A = a (b A)
1A = A .8
תכונות של שחלוף מטריצות
לכל שתי מטריצות Amxn ו- Bmxn מעל שדה F, וסקלר a ב F, מתקיימים השוויונים הבאים
1. (A + B)t = At + Bt
2. (At)t = A
3. (a A)t = a At
כפל מטריצות
כפי שציינו למעלה המכפלה של מטריצות A ו - B שתכתב AB מסובכת מעט.
ולכן כדי להבהיר את הנושא בצורה הטובה ביותר נתחיל במקרים פרטיים.
-
המכפלה B ∙ A של מטריצת שורה A ומטריצת עמודה B בעלות מספר זהה של איברים מוגדרת כך:
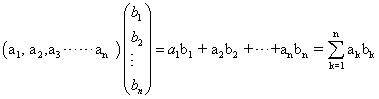 |
א) שהמכפלה B ∙ A היא סקלר(כלומר מספר)
ב) מכפלה זו מוגדרת רק כאשר ל- A ול – B אותו מספר איברים.
דוגמא
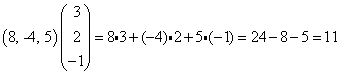
2. לכל שתי מטריצות מעל שדה F, המקיימות Amxk ו- Bkxn נגדיר את הכפל בין שניהם באופן הבא:
Amxk ∙ Bkxn = Cmxn