תלות וקטורים
תכונות במרחב התלת מימדי:
|
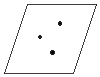
1) כל שלוש נקודות שאיינן על אותו ישר קובעות מישור אחד ויחיד
|
 |
2) דרך כל שתחי נקודות עובר ישר, ולכן עבור כל שתי נקודות במישור הישר שעובר דרכן נמצא
במישור ולכן גם כל הנקודות שעליו.
|
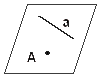
3) כנגד כל ישר a ונקודה A שאינה נמצאת על ישר זה עובר מישור אחד ויחיד.
|
 |
|
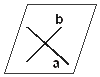
4) שני ישרים שנחתכים, קובעים מישור אחד ויחיד.
|
 |
הגדרה : יהיו a ו b שני ישרים, הישרים a ו b יקראוו מקבילים ונסמן a||b אם הם באותו מישור ואין
להם אף נקודה משותפת או אם הם מתלכדים (כלומר ישר נחשב מקביל לעצמו).
|
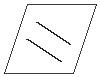
5) שני ישרים מקבילים קובעים מישור אחד ויחיד.
|
 |
6) חיתוך של שני מישורים הוא ישר.
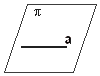
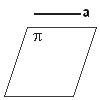
| הגדרה : ישר a מקביל למישור |  |
אם אין לישר ולמישור אף נקודה משותפת או אם הישר נמצא |
|
במישור.
|
  |
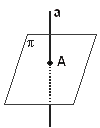
| אם הישר a חותך את המישור |  |
הנקודה המשותפת להם נקראת נקודת החיתוך. |
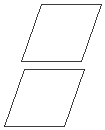
הגדרה : שני מישורים נקראים מישורים מקבילים אם אין להם אף נקודה משותפת או אם הם
מתלכדים.
תכונות ההקבלה :
| (א) יהי a ישר המקביל למישור |  |
. כל מישור העובר דרך הישר a חותך את המישור |  |
בישר b |
המקביל לישר a.
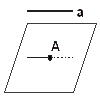
| (ב) יהי |  |
מישור ו A נקודה במישור | 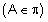 |
, יהי a ישר שאינו במישור המקביל לו, אזי דרך |
|
הנקודה A עובר ישר יחיד המקביל לישר a .
|
 |
| (ג) יהי A ישר במישור |  |
ויהי B ישר מחוץ למישור המקביל ל- A , אזי הישר B מקביל למישור. |
(ד) עבור כל שני מישורים מקבילים ניתן למצוא לפחות ישר אחד בכל מישור כך שישרים אלו מקבילים.
| (ה) יהיו a ו b שני ישרים נחתכים, ויהי |  |
מישור המקביל להם, אזי הוא מקביל גם למישור |
העובר דרכם.
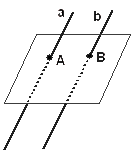
| (ו) יהיו a ו b שני ישרים מקבילים אזי אם a חותך את המישור |  |
בנקודה (A) גם הישר b יחתוך |
|
את המישור בנקודה.
|
 |
הגדרה : ישרים יקראו מצטלבים אם אין להם אף נקודה משותפת והם לא נמצאים באותו מישור.

