הגדרת מישור:
|
מקום גאומטרי של כל הנקודות |
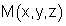 |
, כך שקיימת נקודה | 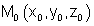 |
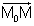 |
מאונך לוקטור נתון |
(A,B,C). |
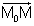 |
הינו וקטור המאונך ל- | 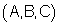 |
. |
| בדומה, כל וקטור היוצא מ- |  |
יהיה מאונך ל- | 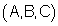 |
ולהיפך, כל וקטור המאונך ל- |
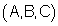 |
יהיה על אותו מישור של | 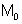 |
| * הערה: אפשר להגדיר מישור כאוסף כל הנקודות המקיימות | 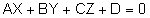 |
| מישור= מרחב הפתרונות של משוואה לינארית אחת ב- | 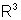 |
מישור הוא תת מרחב ממימד 2 או הזזה שלו. מישור העובר דרך 0 הוא מרחב הפתרונות של משוואה
הומוגנית (לא הומוגנית לא עובר דרך ה-0)
וקטור
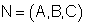
המאונך למישור נקרא נורמל.

