שני ישרים ax+by+c=0 זהים (מתלכדים)אם משוואה אחת מתקבלת
dx+ey+f=0 מהשניה ע"י הכפלה בסקלר.
טענה-הוקטור(a,b) מאונך לכל וקטור המונח על הישר ax+by+c=0 (אותם a ו b)
הוכחה:הצגה פרמטרית של ישר הוא
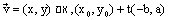
מונח על הישר
| הוא מקיים | 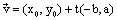 |
נבדוק האם(a,b) מאונך לוקטור (b,a-)המונח |
| על הישר | 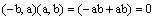 |
כדרוש. |
מסקנה:שני ישרים מקבילים אם המקדמים של x וy זהים עד כדי כפל בקבוע.
| הוכחה: יהיו | 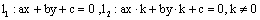 |
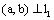
עפ"י טענה קודמת וכן
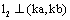
עפ"י אותה טענה ,כמוכן (a,b)ו( k(a,b
|
נמצאים על אותו ישר (בעלי אותו כיוון )ומאונכים לישר אחר ולכן מקבילים. |

