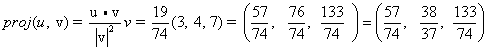פתרון תרגיל מס' 2
פתרון שאלה מס' 1
בצע ראשית את ההכפלה בסקלרים ואז את חיבור הוקטורים
א) 3u - 4v = 3(2, -7, 1) - 4(-3, 0, 4) = (6, -21, 3) + (12, 0, -16)
ב) 2u + 3v - 5w = 2(2, -7, 1) + 3(-3, 0, 4) - 5(0, 5, -8)
=(4, -14, 2) + (-9, 0, 12) + (0, -25, 40)
=(4 - 9 + 0, -14 + 0 - 25 , 2 + 12 + 40 )
= (-5 , -39, 54)
פתרון שאלה מס' 2 -ב
בצע ראשית את ההכפלה בסקלרים ואז את חיבור הוקטורים:
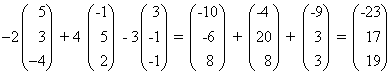
פתרון שאלה מס'3 - ב
מאחר ששני הוקטורים שווים הרכיבים המתאימים שווים זה לזה.
לכן נכפיל בסקלר x ונקבל (4, y ) = x (2, 3) = (2x, 3x). נשווה רכיבים מתאימים
y = 3x 4 = 2x
נפתור את המשוואות הלינאריות עבור x ו- y : x = 2, y = 6.
פתרון שאלה מס' 4
הכפל את הוקטורים מימין בסקלרים הנעלמים ואז חבר:
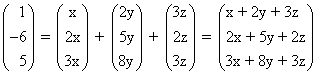
השווה רכיבים מתאימים, וצמצם את המערכת לצורה מדורגת:
x + 2y + 3z = 1
2x + 5y + 2z = -6
3x + 8y + 3z = 5
x + 2y + 3z = 1
y - 4z = -8
2y - 6z = 2
x + 2y + 3z = 1
y - 4z = -8
2z = 18
המערכת היא משולשת, והצבה לאחור נותנת את הפתרון היחיד:
z = 9 , y = 28 , x = -82
פתרון שאלה מס' 5
אנו רוצים לבטא את v בצורה v = xu1 + yu2 + zu3 כאשר x, y, z עדיין נעלמים. כך אנו מקבלים:
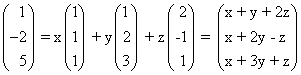
יותר נוח לכתוב את הוקטורים כעמודות מאשר כשורות כאשר יוצרים קומבינציות לינאריות.
מהשוואת רכיבים מתאימים נקבל:
x + y + 2z = 1 x + y + 2z = 1 x + y + 2z = 1
x + 2y - z = -2 או y - 3z = -3 או y - 3z = -3
x + 3y + z = 5 2y - z = 4 5z = 10
הפתרון היחיד של התבנית המשולשת הוא x = -6, y = 3, z = 2 ועל-כו:
v = -6u1 + 3u2 + 2u3
פתרון שאלה מס' 7
היזכר ש- u3, u2, u1 תלויים או בלתי תלויים ליניארית בהתאם לכך אם למשוואה הוקטורית
xu1 + yu2 + zu3 = 0 יש פתרון השונה מאפס או רק פתרון האפס.
אם יש רק פתרון האפס – הוקטורים בלתי תלויים ליניארית
אם יש פתרון שונה מאפס – הוקטורים תלויים ליניארית.
על- כן ראשית השווה קומבינציה ליניארית של הוקטורים לוקטור האפס:
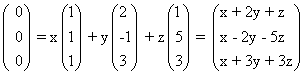
השוה רכיבים מתאימים זה לזה, וצמצם את המערכת לצורה מדורגת:
x + 2y + z = 0 x + 2y + z = 0 x + 2y + z = 0
x - y -5 z = 0 או -3 y - 6z = 0 או y + 2z = 0
x + 3y + 3z = 0 = 0 y + 2z
למערכת בצורה המדורגת יש משתנה חופשי, על כן למערכת יש פתרון השונה מאפס ומכאן שהוקטורים המקוריים תלויים לינארית .
אין צורך לפתור את המערכת כדי לקבוע תלות או אי תלות לינארית, צריך
רק לודא אם קיים פתרון השונה מאפס
פתרון שאלה מס' 10
פתרון שאלה מס' 12
ראשית מצא את |w|2 = w ∙ w = 42 + (-2)2 + (-3)2 + 82 = 16 + 4 + 9 + 64 =93
חלק כל רכיב של w ב- |w| = √93 וקבל:
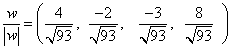
פתרון שאלה מס' 15
ראשית מצא:
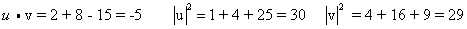
אז:
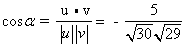
פתרון שאלה מס' 16
ראשית מצא u ∙ v = 3 - 12 + 28 = 19 ו- |v|2 = 9 + 16 + 49 = 74
אז: