מטריצות ריבועיות
כאמור, מטריצה ריבועית היא מטריצה שמספר שורותיה שווה למספר עמודותיה.
על מטריצה ריבועית n x n נאמר שהיא מסדר n ונקרא לה מטריצה n- ריבועית.
כמו שלמדנו לא כל שתי מטריצות ניתנות לחיבור או הכפלה. אך אם דנים רק במטריצות ריבועיות מסדר נתון n כלשהו, בעיה זו אינה מתעוררת.
הפעולות של חיבור, הכפלה, כפל בסקלר ושחלוף ניתנות לבצוע על כל מטריצה n x n והתוצאה היא שוב n x n .
דוגמא
תהיינה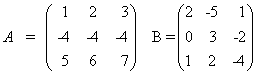 
אזי A ו- B הן מטריצות
ריבועיות מסדר 3.
כמו כן:
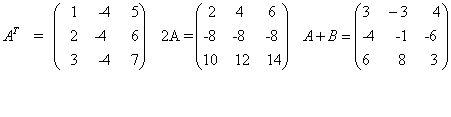
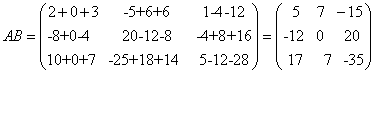
הן מטריצות ריבועיות מסדר 3.
מטריצות מתחלפות
מטריצות A ו- B נקראות מתחלפות אם AB=BA
תנאי זה מתקיים רק לגבי מטריצות ריבועיות מאותו הסדר.
למשל נניח :
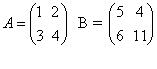
אלכסון ועקבה
נגדיר מהם אלכסון ועקבה של מטריצה A .
תהי A מטריצה n ריבועית.
האלכסון הראשי של מטריצה A מורכב מהאיברים a11, a22,...ann
העקבה של מטריצה A שנסמן ב- tr A היא סכום איברי האלכסון הראשי, כלומר:
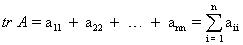
תכונות של עקבה של מטריצה:
נניח ש Aו – B מטריצות n ריבועיות ו-k הוא סקלר אזי:
א) tr (A + B ) = tr A + tr B
ב) tr kA = k * tr A
ג) tr AB = tr BA
ניתן בקלות להוכיח תכונות אלו, ואת ההוכחות נשאיר לכם כתרגיל!
גולשים מקוונים: 1