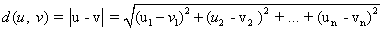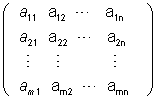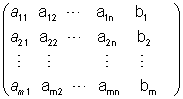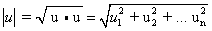המשך מילון מונחים
מערכת של m משוואות לינאריות ב - n נעלמים - מערכת מהצורה:
|
a11X1 + a12X2 + ... + a1nXn = b1 b2 = a21X1 + a22X2 + ... +a2nXn . . . am1X1 + am2X2 + ... + amnXn = bm |
כאשר X1,X2, ...Xn הם הנעלמים.
ו aij (, n ³ j ³11 m ³ i ³) הם מקדמי המשואה.
ו b1, b2, b3 ...bn הם המקדמים החופשיים
מערכות שקולות - אם הן בעלות בדיוק אותם פתרונות בדיוק.
מרחב n - קבוצת כל ה-n-יות של מספרים ממשיים המסומנת ב-Rn
המכפלה הסקלרית או הפנימית של u ו- v , שתסומן ב- u∙v, , היא הסקלר המתקבל מחבור מכפלות הרכיבים המתאימים.
|
u∙ v = u1v1 + u2v2 + ... + unvn |
מרחב- n אויקלידי - המרחב Rn עם הפעולות חיבור וקטורים, כפל בסקלר, ומכפלה פנימית
המרחק בין וקטורים u ו- v שנסמנו ב- d(u, v) מוגדר כ:
|
|
מטריצה - מסדר m x n היא טבלת מספרים (מערך מלבני) עם m שורות ו- n עמודות.
מטריצת המקדמים היא:
|
|
מטריצת המקדמים החופשיים היא:
|
|
מטריצת המקדמים המורחבת היא:
|
|
מטריצה ריבועית מסדר n – מטריצה שבה מספר השורות שווה למספר העמודות
ושווה ל – n.
מטריצת האפס – מטריצה שכל איבריה אפסים. מטריצה זו מסומנת ב- O.
מטריצה אלכסונית – מטריצה ריבועית שכל האיברים פרט לאלכסון הראשי הם אפסים.
מטריצה זו מסמנים ב- diag(a11, a22,...ann)
מטריצה סקלרית – מטריצה אלכסונית שכל איברי האלכסון שווים זה לזה.
מטריצת יחידה – מטריצה סקלרית שבה איברי האלכסון שווים ל- 1.
את מטריצת היחידה מסדר n מסמנים ב- In .
מטריצה סימטרית – מטריצה ריבועית היא סימטרית אם A = At
כלומר aij = aji. לכל i ו- j.
מטריצה אנטי סימטרית – מטריצה ריבועית היא אנטי-סימטרית אם -A = At
וכל האיברים על האלכסון הראשי שווים ל- 0.
כלומר aij = aji- לכל i ו- j.
מטריצה משולשת עליונה(תחתונה) - היא מטריצה ריבועית שכל איבריה מתחת (מעל) האלכסון הראשי הם אפסים.
מטריצות מתחלפות - מטריצות A ו- B נקראות מתחלפות אם AB=BA
מרחב וקטורי V מעל שדה K - הוא קבוצה לא ריקה של איברים הנקראים וקטורים, שבה מוגדרת פעולת החיבור המתאימה לכל שני וקטורים u, v השייכים ל- V וקטור u + vגם שייך ל-V וכן מוגדרת פעולת הכפל בין איבר u ב- V לבין איבר k ששיך ל-K וקטור ku גם שייך ל- V
מטריצה מדורגת - מטריצה שבה התנאים הבאים מתקימים:
א) כל שורות האפסים, אם יש כאלה הן בתחתית המטריצה.
ב) כל איבר מוביל שונה מאפס הוא מימין לאיבר המוביל השונה מאפס בשורה
הקודמת.
מטריצה קנונית - מטריצה שבה התנאים הבאים מתקימים:
א) כל שורות האפסים, אם יש כאלה הן בתחתית המטריצה.
ב) כל איבר מוביל שונה מאפס הוא מימין לאיבר המוביל השונה מאפס בשורה
הקודמת.
ג) כל איבר מוביל השונה מאפס הוא 1
ד) כל איבר מוביל השונה מאפס הוא האיבר היחיד השונה מאפס בעמודתו.
מטריצה הפיכה - אם קיימת מטריצה B כך ש:
|
|
מטריצת הילברט - מטריצה A שאיבריה ![]()
מטריצה אורתוגונלית - אם AAT = ATA = I
נ
נעלם המוביל - זה הנעלם הראשון במשוואה עם מקדם שונה מאפס.
נרמול - התהליך של מציאת וקטור היחידה.
הנורמה (או האורך) - של וקטור u, שתסומן ב- | u | מוגדרת כשורש הריבועי
האי- שלילי של u∙ u
|
|