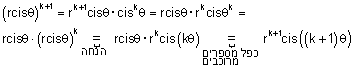משפט דה-מואבר : לכל מספר שלם n מתקיימת הנוסחה הבאה

הוכחה באינדוקציה: נוכיח באינדוקציה ל- n טבעי.

בדיקה: עבור n = 1   :

וזה מתקיים

           עבור n = 2   :                    

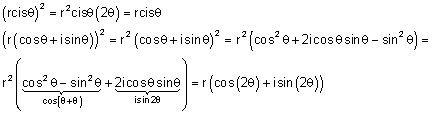
וזה גם מתקיים

הנחה:  נניח כי הטענה נכונה עבור n = k טבעי כלשהו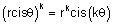
ונוכיח עבור  n = k+1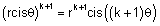