וקטורים ומשוואות לינאריות
שני מושגים חשובים העוסקים בוקטורים, קומבינציות לינאריות ותלות ליניארית, קשורים קשר הדוק למערכות של משוואות לינאריות.
קומבינציות לינאריות
התבונן במערכת לא- הומגנית של m משוואות ו- n נעלמים:
a11X1 + a12X2 + ... + a1nXn = b1
a21X1 + a 22 X 2 + ... + a2nXn = b2
.
.
.
am1X1 + am2X2 + ... + amnXn = bm
מערכת זו שקולה למשוואה הוקטורית הבאה:
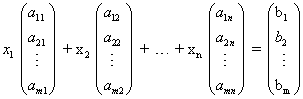
כלומר למשוואה הוקטורית:
x1u1 + x2u2 + ... + xnun = v
כאשר u1, u2 , ... un ו- v הם וקטורי העמודה שלעיל בהתאמה.
אם למערכת יש פתרון , אז אומרים ש- v היא קומבינציה לינארית (צרוף לינארי) של הוקטורים ui.
דוגמא
נניח
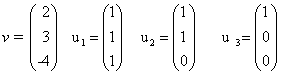
אז v הוא קומבינציה לינארית של u1, u2, u3 מאחר שלמשוואה הוקטורית ( או למערכת)
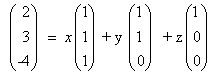
יש פתרון x = -4, y = 7, z = -1
במילים אחרות v = -4u1 + 7u2 - u3 :
תלות לינארית
התבונן המערכת ההומוגנית של m משוואות ו- n נעלמים:
a11X1 + a12X2 + ... + a1nXn = 0
a21X1 + a22 X 2 + ... + a2nXn = 0
.
.
am1X1 + am2X2 + ... + amnXn = 0
מערכת זו שקולה למשוואה הוקטורית הבאה:
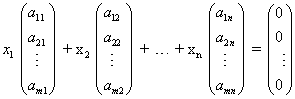
כלומר למשוואה הוקטורית:
x1u1 + x2u2 + ... + xnun = 0
כאשר u1, u2 , ... un הם וקטורי העמודה שלעיל בהתאמה.
כעת אם למערכת ההומוגנית יש פתרון שונה מאפס, הוקטורים u1, u2 , ... un נקראים תלוים לינארית. מאידך אם למערכת יש רק פתרון האפס, אז הוקטורים נקראים בלתי- תלוים לינארית.
דוגמאות
א) הפתרון היחיד ל- 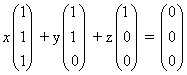 או
או 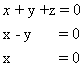
הוא פתרון האפס x = 0, y = 0, z = 0 על כן שלושת הוקטורים בלתי תלוים לינארית.
ב) למשוואה הוקטורית 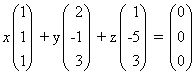 או
או 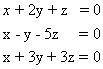
יש פתרון שונה מאפס (1, 2- , 3)
x = 3, y = -2, z = 1 כלומר
על – כן שלושת הוקטורים תלוים לינארית
