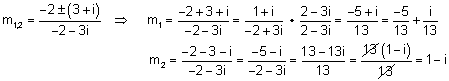| בהנתן משוואה ריבועית של מספרים מרוכבים |  |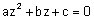
כאשר a,b,c מספרים מרוכבים |
| ו- |  |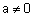
.מקיימים המקדמים את נוסחאות וייטה כך שאם |  |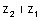
שורשי המשוואה אזי: |
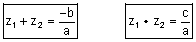
| ועל כן ניתן לרשום את המשוואה הריבועית באופן הבא: |  |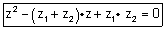
הערה: אם למשוואה הריבועית
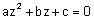
שמקדמיה a,b,c הם מספרים מרוכבים ,יש
שורש מרוכב לא ממשי אזי גם השורש השני מרוכב והוא הצמוד לשורש הראשון.
| כלומר אם |  |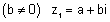
אזי השורש השני הוא |  |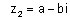
| דוגמה: מצא את m אם |  |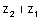
הם שורשי המשוואה |  |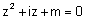
והם מקיימים | : |
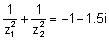
פתרון:
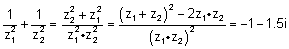
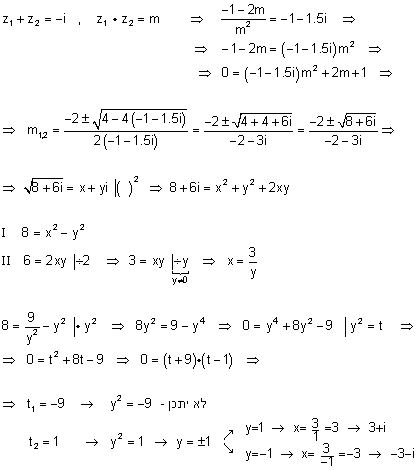
נציב בחזרה את אחד השורשים בנוסחת השורשים עבור m ונקבל:
גולשים מקוונים: 5