בפתרון של משוואה ריבועית ראינו הרבה פעמים שלמשוואה x2 = -a
ולכן לא קיים מספר ממשי x עבורו x2 = -a. על מנת לפתור משוואות מהסוג הזה נצרף למספרים הממשיים "מספר" חדש אשר יסומן ע"י i ומוגדר באופן הבא:
(למשל x2 = -1). כאשר a ו x מספרים ממשיים אין פתרון כיוון ש- x2
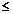
0 .
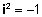 |
או | 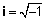 |
i נקרא מספר מדומה |
מספר מדומה: מספר מדומה שצורתו bi ( או ib) כאשר b הוא מספר ממשי ו - i
מספר מדומה המקיים
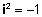 .
.
מספר מרוכב: מספר שצורתו a+bi, כאשר a ו b הם מס' ממשיים.
החלק הממשי: a נקרא החלק הממשי של המספר a+bi.
החלק המדומה: b נקרא החלק המדומה של המספר a+bi.
המשפט היסודי: לכל משוואה אלגברית ממעלה n (כאשר n מספר טבעי) מהצורה:
a0 + a1x + an-1xn-1 +...+ anxn
(0
.(an
שבה המקדמים: an, an-1, ... ,a1,a0 הם מספרים מרוכבים, יש לפחות שורש אחד מרוכב.

