פעולות חשבון שבין המספר i למספרים ממשיים דומות לפעולות החשבון שבין שני משתנים. שני מספרים מרוכבים a+bi , c+di יהיו שווים, כלומר: a+bi = c+di אם a = c וגם b = d. ולהפך: אם a = c וגם b = d אזי המספרים המרוכבים: a+bi, c+di שווים.
חיבור: (חיסור באותו אופן, שכן חיסור זוהי פעולת חיבור של המספר הנגדי:
) (a+bi) – (c+di) = (a+bi) + (-c-di)
מחברים את הממשיים לחוד ואת המדומים לחוד:
^מדומה ^ממשי
כפל: כופלים על-פי חוק הפילוג המורחב:
(a+b)(c+d) = ac+ad+bc+bd
כאשר i2 = -1 :
^ מדומה ^ ממשי
הערה: כאשר רוצים לייצג מספר ממשי ע"י מספר מרוכב ה- b יהיה 0 :
a = a + 0 * i
|
דוגמאות: |
נתון | 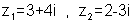 |
| א) | 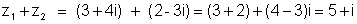 |
| ב) | 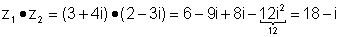 |
| המספר הצמוד: המספר הצמוד למספר z = a+bi הוא | 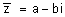 |
| סימון: המספר הצמוד ל- z יסומן ע"י | 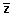 |
דוגמאות:
| א) מצא את המספר הצמוד ל - | 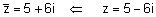 |
| ב) נתון: z = 2 - 4i מצא את המספר המרוכב - | 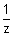 |
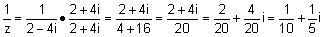
| טענה: | 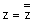 |
| הוכחה: יהי z = a + bi אזי | 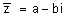 |
ולכן - | 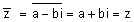 |

