שדה
לפני שנתחיל ללמוד על מרחבים וקטוריים נזכיר תחילה את המושג שדה.
שדה הוא קבוצה של איברים אשר מכילה לפחות שני איברים עם שתי פעולות בינאריות חיבור וכפל בעלות תשע התכונות הבאות המתקיימות עבור כל בחירה של איברים מהקבוצה a,b,c:
א) החיבור הוא קומוטטבי a+b = b+a : (חוק החילוף) ב) החיבור הוא אסוציאטיבי :+ c (a + (b + c) = (a + b (חוק הקיבוץ) ג) 0 + a = a, 0 הוא המספר היחיד בעל תכונה זו ( 0 איבר אדיש (נטרלי) ביחס לחיבור). ד) לכל a יש איבר יחיד a - , כך ש- a + (-a) = 0 ( הפעולה b + (-a) , כלומר b - a היא פעולת החיסור). ה) הכפל הוא קומוטטבי: a b = b a. ו) הכפל הוא אסוציאטיבי : c (a (b c) = (a b . ז) a*1= a ו- 1 הוא האיבר היחיד שמקיים זאת. ( 1 איבר אדיש (נטרלי) ביחס לכפל). ח) לכל a ששונה מ-0 יש איבר יחיד a-1 , כך ש- a*a-1 = 1 (איבר הופכי) ט) מתקיים חוק הפילוג: (a + b) c = a*c + b*c (דסטריבוטיביות)
דוגמאות
א) שדה המרוכבים C, שדה הממשי R, ושדה הרציונלי Q.
ב) הקבוצה Z אינה שדה כי רק ל- 1 ול- 1- יש איבר הופכי.
ג) קבוצת המספרים הזוגיים ![]() היא לא שדה. (בדקו!)
היא לא שדה. (בדקו!)
ד) נתונה קבוצת המטריצות 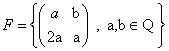 נוכיח ש- F שדה.
נוכיח ש- F שדה.
צריך להוכיח את כל תשע התכונות של שדה.
נוכיח ש-F סגורה לגבי חיבור וכפל, כלומר סכום ומכפלה של שתי מטריצות מ-F הן מטריצות ב-F.
תהיינה ![]()
![]()
חיבור וכפל של מטריצות מ-F מקיימים את התכונות א'-ז' ו-ט'. נבדוק את תכונה ח'.
מספיק להראות שכל מטריצה A השונה מ- 0 הפיכה ב-F , ואמנם אם A שונה מ-0 הדטרמיננט A = a2 - 2b2 שונה מ- 0 לכל a ,b רציונאליים, לכן היא הפיכה.
כל התכונות מתקיימות ולכן F שדה.
עכשיו נוכל להסביר את המושג מרחבים וקטורים!
