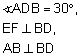דוגמה:

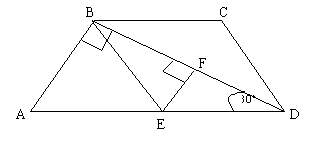
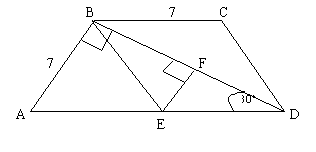
בטרפז ABCD נתון:

 7 ס"מ  =  AB=BC,

הקטע BE הוא תיכון ליתר במשולש ישר זוית

א. חשב את אורך הבסיס AD.

ב. חשב את אורך התיכון BE.

ג. חשב את אורך הקטע FD.

פתרון: תחילה נסמן את הנתונים על גבי השרטוט.

א. על מנת למצוא את AD נחפש משולש ישר זוית בו AD הוא צלע.

משולש

הוא משולש ישר זוית שזויותיו החדות הן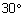

ו

ולכן על פי משפט

פיתגורס: היתר שווה לפעמיים אורך הניצב שמול הזוית בת ה-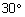

.

 

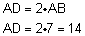
ב. BE תיכון ליתר AD במשולש ישר זוית		ולכן על פי משפט שווה למחצית היתר,
כלומר-

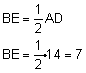
ג. על מנת לחשב את אורך הקטע FD נחפש משולש ישר זוית ב- EF הוא צלע.

נסתכל על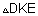

הצלע 7ס"מ = DE, כיון ש- BE תיכון ליתר 14 ס"מ = AD . BE

מחלקת את AD לשני חלקים שווים.

את EK נמצא על פי המשפט - במשולש ישר זוית שזויותיו החדות הן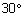

ו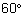

הניצב

שמול הזוית בת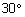

שווה למחצית היתר ולכן -

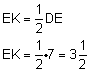
כעת נשתמש במשפט פיתגורס ונקבל-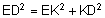
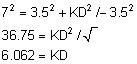