|
עורכים סידרה של ניסויי ברנולי עד לקבלת "הצלחה" בפעם הראשונה .
נגדיר את המשתנה המקרי הבא, G - מספר הניסויים עד לקבלת הצלחה בפעם הראשונה (כולל).
דוגמאות למשתנה המקרי G :
נשים לב כי בניגוד למקרה הקודם (ההתפלגות הבינומית) , בו מספר הניסויים נקבע מראש, בכל הדוגמאות האלו , מספר הניסויים עצמו הינו משתנה מקרי.
פונקצית ההסתברות של G , מתארת את ההסתברות של המאורע :
"ההצלחה הראשונה תקרה בניסויי ה - k "
|
|
פונקציה זו נקראת פונקצית ההסתברות הגיאומטרית.
פונקצית ההתפלגות שלה היא:
|
|
זוהי ההסתברות כי ההצלחה הראשונה תקרה עד הניסוי ה- k. (דהיינו בניסוי הראשון או השני או השלישי עד הניסוי ה- k .
|
|
התוחלת של G היא :
|
|
השונות של G היא :
|
|
ספינה יורה טילים לספינת אויב וידוע כי ההסתברות לפגיעה של טיל בודד הינה קבועה: p=0.7.
א. מה ההסתברות כי ספינת האויב תיפגע מהטיל החמישי?
ב. כמה טילים יש לירות כדי שהסתברות הפגיעה תהיה 0.75?
ג. אם עלות ירי של טיל היא 8000 שקלים , מה תהיה תוחלת עלות השמדת המטרה?
|
|
א. ההסתברות לפגיעה ראשונה בטיל החמישי:
ב. נניח שמספר הטילים הדרוש הוא k (k אינו ידוע). אנו מעוניינים למצוא k כזה, שההסתברות שתהיה פגיעה ראשונה עד לטיל ה- k היא 0.95.
דהיינו:
kנמצא את :
|
|
נוציא log משני אגפי המשוואה ונקבל:
דהיינו : דרוש ירי של 3 טילים כדי שההסתברות לפגיעה תהיה מעל 0.95.
ג. תוחלת עלות השמדת המטרה תהיה תוחלת מס' הטילים הדרוש כדי להשמידה כפול עלות הטיל (8000 שקלים). ידוע כי:
לכן תוחלת עלות השמדת המטרה היא : |
|
 |
||
יום שבת 26 באפריל 2025
|
|
|
|||||||||||||||||||||||||||||

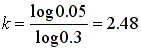
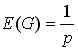 .
.