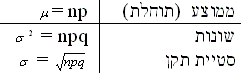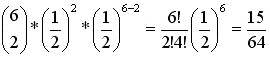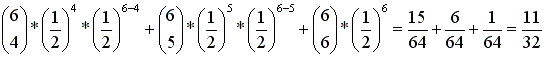|
עורכים סידרה של ניסויים אקראיים ובכל ניסוי עשויה תוצאה מסוימת להתרחש או לא להתרחש. אם התוצאה קרתה נאמר שהניסוי הסתיים בהצלחה ואם היא לא קרתה נאמר שהניסוי הסתיים בכישלון.
ניסוי אקראי כזה , העשוי להסתיים באחת משתי תוצאות אפשריות (הצלחה או כישלון) נקרא : ניסוי ברנולי .
דוגמאות לניסויי ברנולי :
נגדיר את המשנה המקרי הבא: |
|
היה כישלון 0 X = קרתה הצלחה 1 |
|
זהו ניסוי ברנולי.
ברור כי אם ההסתברות להצלחה בניסוי בודד היא p , אזי פונקצית ההסתברות של x היא :
P(x=1) = p
P(x=0) = 1-p
נניח עתה כי נערכת סידרה של n ניסויי ברנולי בלתי תלויים (דהיינו התוצאה בניסוי אחד אינה משפיעה על התוצאה בניסוי אחר בסדרה) , וההסתברות להצלחה בכל ניסוי היא קבועה ושווה ל - p. למשל: נערכות n קליעות למטרה , כאשר ההסתברות לפגיעה הינה p בכל קליעה.
פונקצית ההסתברות הבינומית היא:
|
|
כאשר:
n מספר הניסויים .
k מספר ההצלחות.
p הסתברות להצלחה בכל ניסוי.
q הסתברות לכישלון כלומר 1-p .
|
|
|
|
ההסתברות לקבלת 2 "פאלי" בדיוק , מתוך 6 הטלות של מטבע הוגן היא:
זאת תוך ניצול נוסחת ההתפלגות הבינומית עם : n=6 , x= 2,p=q=0.5 |
|
ההסתברות לקבלת 4 "פאלי" לפחות , מתוך 6 הטלות של מטבע הוגן היא:
|
|
במאה הטלות של מטבע הוגן מספר ה"פאלי" הממוצע הוא :
np = 100*0.5 = 50 =
זוהי תוחלת מספר ה"פאלי" מתוך מאה הטלות המטבע.
סטיית התקן היא :
|
|
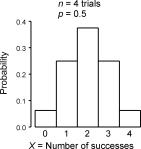
ציור של התפלגות בינומית |
|
 |
||
יום שבת 26 באפריל 2025
|
|
|
|||||||||||||||||||||||||||||