אנרגיית קפיץ
נתבונן במקרה הבא:
גוף הנע במהירות v (ולכן בעל אנרגיה קינטית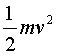 
) נתקע בקפיץ. הקפיץ בולם את הגוף ומתכווץ. "נעצור" את התמונה ברגע בו מהירותו של הגוף אפס, וננסה להבין היכן נמצאת האנרגיה הקינטית שהיתה לגוף בהתחלה.
שוב, נעשה זאת מתוך חישוב העבודה שהפעיל הקפיץ על הגוף.
הקפיץ, כזכור, מפעיל כח של 
על הגוף.
אך כאן כבר מסובך להשתמש בנוסחת העבודה
בצורה פשוטה, כיוון ש- F-, הכח שמפעיל הקפיץ, אינו קבוע אלא משתנה עם x, הלא הוא מידת ההתכווצות של הקפיץ!
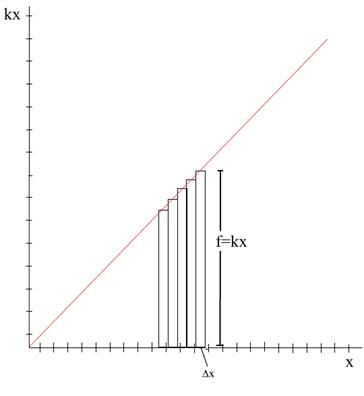
כדי לפתור את הבעיה נסתכל בגרף המראה את הכח שמפעיל קפיץ (הציר האנכי) לעומת שינוי באורכו (הציר האופקי). נצייר מלבנים קטנים על הגרף (בציור מתוארים כמה מלבנים לדוגמה). גובהם של המלבנים הוא הכח אותו מפעיל הקפיץ ורוחבם מצוייר סביב שיעור השינוי באורך הגורם לאותו כח. העבודה שמפעיל הקפיץ באותו שינוי אורך המצויין ע"י המלבן, היא גובה המלבן כפול רוחבו 
.
אם נעשה את המלבנים צרים מספיק, נראה ששטחם ממלא משולש ישר זווית, שהיתר שלו הוא הגרף האדום, מימין הוא תחום ע"י המלבן הגבוה ביותר, ומלמטה הוא תחם ע"י הציר האופקי. שטחו של המשולש הזה הוא הגובה כפול הבסיס חלקי שתים.
מכאן נובע, שסכום שטחי המלבנים, שהוא גם סכום העבודות שהם מייצגים הוא
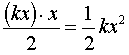
כאשר x הוא אורך הצלע המקבילה לציר האופקי.
זוהי העבודה שעושה קפיץ שמתכווץ בשיעור x. ולכן זהו שיעור האנרגיה האגורה בקפיץ.
גולשים מקוונים: 6