חוקי קירכהוף
ישנם מעגלים מורכבים יותר מאלו שדנו בהם עד עכשיו. למשל, מעגלים עם נגדים המחוברים לא בטור ולא במקביל, או עם יותר ממקור מתח אחד. לפתירת מעגלים אלו ניעזר בשני חוקי קירכהוף.
חוק הזרמים של קירכהוף
ידוע שכאשר זרם מגיע להתפצלות לשני מסלולים אחרים, אזי סכום הזרמים המתפצלים שווה לזרם המקורי שהיה לפני ההתפצלות. אך מה קורה כאשר נכנסים לצומת יותר מזרם אחד?
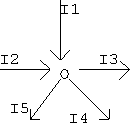
סך כל הזרמים הנכנסים לצומת, שווה לסך כל הזרמים היוצאים מהצומת.
ולכן לפי הדוגמא שלנו, I1 + I2 = I3 + I4 + I5.
חוק זה נקרא חוק הזרמים של קירכהוף: סך כל הזרמים הנכנסים לצומת, שווה לסך כל הזרמים היוצאים מהצומת. נסמן זרם נכנס ב – Ii וזרם יוצא ב – Io ובניסוח מתמטי נקבל:
∑Ii = ∑Io
חוק המתחים של קירכהוף (חוק העניבה)
בין שני הצדדים של מקור המתח יש הבדל בפוטנציאלים. הפוטנציאל בצד ה (-) נמוך מהפוטנציאל בצד ה – (+) בלי קשר להתנגדות הפנימית. ולכן כיוון המתח הוא
מה (-) אל ה – (+).
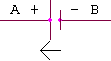
כיוון מקור המתח
אם נרצה לחשב את הפרש הפוטנציאלים בין A ל – B הכיוון יהיה נגד הכיוון של מקור המתח, ולכן נוסיף לפניו את הסימן (-).
UAB = - |E|
אם הכיוון היה מ – B ל – A החישוב היה בכיוון מקור המתח
UAB = |E|
מכיוון שלכ.א.מ יש שני כיוונים נגדיר אותו כוקטור. כיוון הוקטור הוא מההדק השלילי של הכ.א.מ אל ההדק החיובי שלו. ולכן,
UAB = - E
בהתאם גם לגבי הזרם. אם החישוב הוא בכיוון הזרם אזי
UAB = IR
ואם החישוב הוא בכיוון מנוגד לכיוון הזרם אזי
UAB = - IR
אם גם הזרם יהיה וקטור עם שני כיוונים אזי
UAB = IR
ואם נכליל את 2 הדוגמאות נקבל:
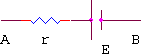
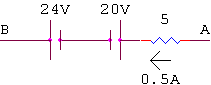
שני מקורות המתח מחוברים בטור, בכיוונים מנוגדים. לכן המתח הוא הפרש המתחים.
UAB = 0.5 · 5 - (24 - 20) = -1.5V
כלומר, כאשר יש יותר ממקור מתח אחד, נחבר את מקורות המתח, אך יש לשים לב לכיוונים. כמו כן, אם יש יותר מנגד אחד, גם אז נעבר את כל הזרמים והנגדים.
ומכאן נקבל ש:
