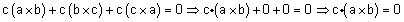| מכפלה מעורבת היא מכפלה סקלרית על מכפלה ויקטורית. |
| טענה- | 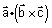 |
הוא סקלר שערכו המוחלט הוא נפח המקבילון הבנוי על | 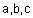 |
||||||
| כאשר |  . . |
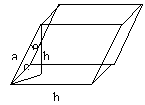
| מקבילון= מקבילית תלת מימדית ונפח המקבילון | 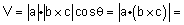 |
||||||||
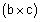 |
הוא וקטור המאונך ל- b ול- c. כלומר: מאונך לבסיס המקבילית זהו הגובה. | ||||||||
 |
הוא הזוית בין h ל-a ולכן היא הזוית בין | 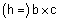 |
ל-a. |
 |
|
| טענה- | א) יהיו | 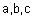 |
וקטורים ב- | 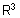 |
, אזי - | 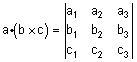 |
| ב) | 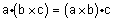 |
| מסקנה- נפח מקבילון הוא הערך המוחלט של הדטרמיננטה: | 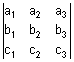 |
| טענה- |  |
הם על אותו מישור | 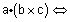 |
| הוכחה- אחד הוקטורים תלוי - לינארית בשנים האחרים |  |
| הם באותו מישור |  |
שניים פותרים את הוקטור השלישי |  |
| מסקנה- אם | 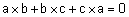 |
, אזי | 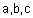 |
וקטורים על אותו מישור (קופלנרמה). |
| הוכחה- | 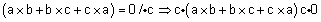 |
||||||||
|
|
|||||||||
| לפי משפט | 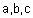 |
על אותו ישר | |||||||
 |
מאונכים ולכן = 0 | 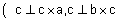 |
|||||||