|
טענה: קיים מישור שמאונך גם ל- |
 |
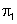וגם ל |  |
הוכחה:
| יהי |  |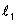
נורמל ל- |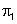
ו- |  |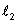
נורמל ל- |  |
| נתבונן במישור שהנורמל שלו הוא |  |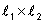
, כלומר קיים מישור המאונך לשני המישורים. |
טענה: קיימת נקודה שבה נפגשים 3 מישורים.
הוכחה:
P נקודת המפגש בין 3 המישורים.
 |
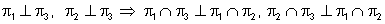
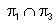נמצא ב- |  |
 |
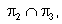נמצא ב- |  |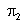
צריך למצוא את הזוית ביניהם.
גולשים מקוונים: 11