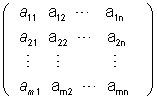מטריצות - מבוא
הפרק השלישי באתר יעסוק במטריצות.
יש קשר הדוק בין מערכת משוואות לבין מטריצות, ולכן כאשר נלמד חלק מהמושגים שקשורים למטריצות, הם יזכירו לכם את המושגים של מערכות משואות לינאריות.
אך אל - דאגה את הכול נראה בהמשך.
אנו נסמן ב- Fmxn את קבוצת המטריצות מסדר m x n ( מטריצות בעלות m שורות ו- n עמודות), שאיבריהן שייכים לשדה F .
בפרק זה F הוא R או C.
אז קדימה לעבודה!
לפני שנתחיל נבין קודם מה זאת מטריצה, ואיך מושג זה מתקשר למערכת משוואות.
מטריצה מסדר mxn היא טבלת מספרים (מערך מלבני) עם m שורות ו n- עמודות
אם נתונה מערכת משוואות:
|
a11X1 + a12X2 + ... + a1nXn = b1 a2nXn = b2 a21X1 + a22X2 + ... + . . . |
אז נסמן ב- A את מטריצת המקדמים והיא:
|
|
aij נקרא האיבר ה- i j או הרכיב ה- i j , והוא מופיע בשורה ה- i ובעמודה ה- j .
מטריצה עם m שורות ו- n עמודות נקראת מטריצה m על n , או מטריצה m x n .
זוג המספרים (m,n) נקרא גודל המטריצה.
נסמן ב- b את מטריצת המקדמים החופשיים והיא:
|
|
ונסמן ב- A| b את מטריצת המקדמים המורחבת והיא:
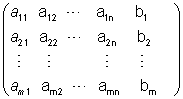
דוגמא
תהי 
. אז A היא מטריצה 
.
שורותיה הן (4, 3-, 1) ו- (2-, 5, 0).
עמודתיה הן 
, 
, ו - 
.
גולשים מקוונים: 13