מטריצות מיוחדות
נביא כאן בקצרה חלק מן ההגדרות של מטריצות מיוחדות, אך בחלק מהם נרחיב את הנושא בפרק של מטריצות ריבועיות.
וקטור שורה – מטריצה בעלת שורה אחת.
וקטור עמודה – מטריצה בעלת עמודה אחת.
מטריצה ריבועית מסדר n – מטריצה שבה מספר השורות שווה למספר העמודות
ושווה ל – n.
מטריצת האפס – מטריצה שכל איבריה אפסים. מטריצה זו מסומנת ב- O.
מטריצה אלכסונית – מטריצה ריבועית שכל האיברים פרט לאלכסון הראשי הם אפסים.
מטריצה זו מסמנים ב- diag(a11, a22,...ann)
מטריצה סקלרית – מטריצה אלכסונית שכל איברי האלכסון שווים זה לזה.
מטריצת יחידה – מטריצה סקלרית שבה איברי האלכסון שווים ל- 1.
את מטריצת היחידה מסדר n מסמנים ב- In .
מסובך? אל דאגה הדוגמאות הבאות ימחישו את ההגדרות.
דוגמאות
א) ב) ג)
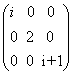
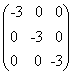
מטריצה א'- היא אלכסונית ונסמנה ב- ( diag(i, 2, i+1 .
מטריצה ב' - היא סקלרית.
מטריצה ג' - היא מטריצת יחידה I4 .
מטריצה סימטרית – מטריצה ריבועית היא סימטרית אם A = At
כלומר aij = aji. לכל i ו- j.
גולשים מקוונים: 2