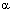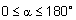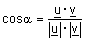מכפלה סקלרית במרחב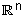

המכפלה סהקלרית בהצגה אלגברית ב-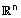

היא הכללה למכפלה הסקלרית עליה דברנו במישור

ובמרחב.

הגדרה : לכל שני וקטורים n מימדיים v , u כאשר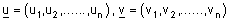

מוגדרת המכפלה הסקלרית באופן הבא :

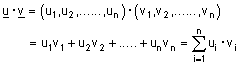הערה : במרחב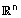

מתקיימים חוק החילוף והפילוג בדומה למישור ולמרחב.

הגדרה : יהיו u וקטור ב-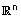

, אזי האורך של u מוגדר באופן הבא -

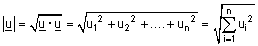
הגדרה : יהיו u , v שני וקטורים אזי : (א) אם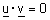

הוקטורים u ו v נקראים ניצבים/ מאונכים.

(ב) אם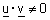

ו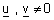

אזי הזוית שבין u ו v

מוגדרת ע"י מספר

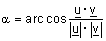
משפט (אי שיוויון קושי שוורץ) :

לכל שני וקטורים u , v ב-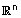

מתקיים: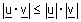

משפט (אי שיוויון המשולש) :

לכל שני וקטורים u , v ב-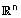

מתקיים: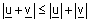

משפט :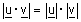

אם ורק אם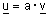

עבור a מסויים.