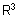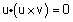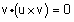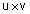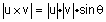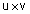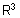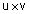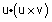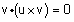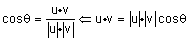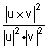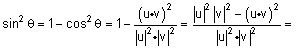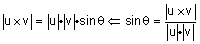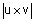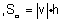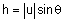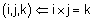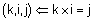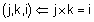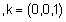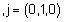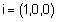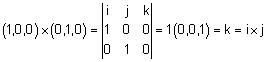משפט תכונות מכפלה וקטורית משפט תכונות מכפלה וקטורית |
|
|
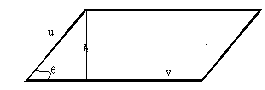
| יהיו u ו- v שני וקטורים ב- |
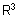 |
ותהי |
 |
הזוית בין וקטורי הכיון שלהם, אזי: |
|
|
|
|
|
| א) |
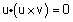 |
|
 |
- מכפלה סקלרית, |
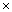 |
- מכפלה וקטורית. |
|
|
|
| |
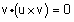 |
|
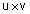 |
מאונך ל- u ול- v וממולא למישור שנוצר על-ידם. |
|
|
|
|
|
| ב) |
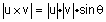 |
|
|
|
|
|
|
|
|
| ג) |
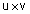 |
, v,u מהווים מערכת ימינית. |
|
|
|
|
|
|
|
| מערכת ימינית: |
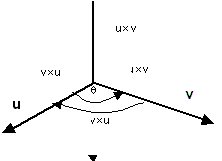 |
|
|
|
|
|
|
|
|
| הוכחה: |
א) מגדירים v, u וקטורים ב- |
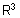 |
מוציאים |
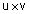 |
לפי הגדרת det, פותרים |
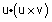 |
| |
ומקבלים 0 בדומה לגבי |
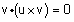 |
. |
|
|
|
|
|
|
| |
ב) ידוע שבמכפל ה סקלרית מתקיים |
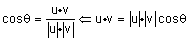 |
|
|
|
|
|
|
|
| |
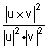 |
עפ"י הגד' |
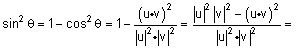 |
|
| |
ולכן |
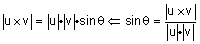 |
|
|
|
|
|
|
|
| |
מסקנה - |
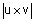 |
הוא שטח המקבילית הבנוי על u, v. |
|
|
|
|
|
|
| |
ג) נבדוק שאיברי הבסיס i,j,k מתנהגים הצורה דומה במערכת ימינית, כלומר נראה ש- |
| |
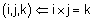 |
מערכת ימינית, |
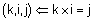 |
מערכת ימינית |
|
|
|
|
|
| |
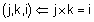 |
מערכת ימינית. |
|
|
|
|
|
|
|
| |
בודקים לפי ההגדרה כלומר- אם |
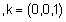 |
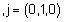 |
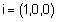 |
|
|
|
|
|
|
| 23-03-04 / 23:13 | עודכן , | 09-03-04 / 22:19 | נוצר ע"י ירון בירנבאום בתאריך |
|
| |
|
|