ישר הוא תמ"ו מימד אחד או הזזה שלו ולכן במישור שהוא מימד 2 אנו משתמשים במשוואה אחת על מנת שמרחב הפתרונות יהיה תת מרחב מימד אחד.
הזזה של תמ"ו-לכל וקטור בתמ"ו מוסיפים וקטור.
במרחב משוואה אחת תתן לנו מרחב פתרונות שהוא תמ"ו מימד 2 או הזזה שלו (וזהו המישור)
ולכן כדי לתאר ישר נשתמש בשתי משוואות.
| דוגמה:נתונה מערכת משוואות | 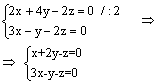 |
| למערכת זו יש אינסוף פתרונות .z משתנה חופשי על כן נציב z=t ונקבל z=t y=t/7 x=5/7t | 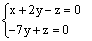 |
| כלומר: | 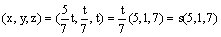 |
| מרחב הפתרונות הוא | 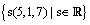 |
זוהי הצורה הפרמטרית של ישר העובר (0,0,0) |
וכוונו (5,1,7).
מסקנה-שתי משוואות בלתי -תלויות לינאריות מגדירות ישר ב r3.
משפט-פתרון כללי של מערכת הומוגנית +פתרון פרטי של מערכת לא הומוגנית =פתרון כללי של מערכת לא הומוגנית.
זוהי משוואה פרמטרית של ישר שכיוונו (a,b,c) העובר דרך (x,y,z).

