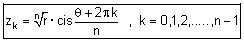שרשי היחידה : נרצא למצוא את n השורשים השונים של המשוואה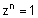

, עבור n טבעי.

עבור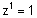

יש פתרון יחיד והוא z=1 , עבור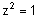

ישנם 2 פתרונות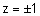

.

ננסה למצוא את 3 הפתרונות של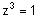

. כיוון ש- z הוא מספר מרוכב נייצג אותו בייצוג קוטבי

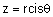ולכן:

            

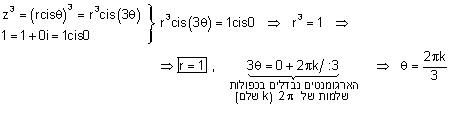
לכן הפתרון הכללי הוא: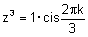

הזווית בתחום: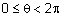

הן: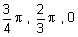

כל שאר הזוויות מתקבלות ע"י תוספת של

כפולות של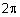

. ולכן ה -k ים המתאימים הם: k = 0,1,2,...,n.

	4	3	2	1	0	: k
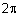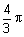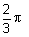.......					0	:

הפתרונות באופן המפורט הן:

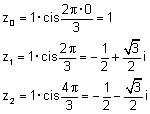הערה:  ניתן לבדוק כי השורשים אכן מקיימים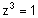

ע"י הצבה.

לפתרון המשוואה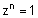

יש שורשים שונים והם: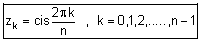

עבור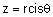

נפתור באותה שיטה. נניח כי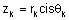

שורש שלו ,אזי צריך להתקיים

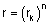ו -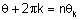

ולכן n השורשים השונים של המספר המרוכב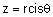

הם: