| משפט:א.יהי |  |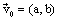
וקטור במישור. |
| איחוד כל ראשי הוקטורים |  |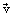
המקיים |  |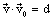
הוא ישר קבוע. |
| ב.כל הנקודות |  |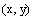
במישור המקיימות |  |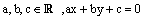
הן הישר |  |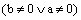
| הוכחה:א |  |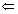
ב |
 |
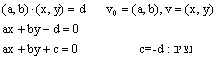| באותו אופן בכיוון ההפוך .כעת נוכיח את נכונות א |
| כיוון א':נראה שכל נק' על ההצגה הפרמטרית מקיימת את א עבור d קבוע נמצא את d. |
| יהי l ישר הנתון בצורה פרמטרית : |  |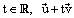
 |
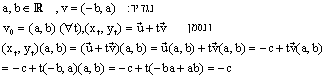| כלומר הראנו שקיים |  |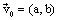
כך שלכל נק' על הישר |  |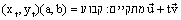
| כיוון ב' תהי |  |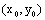
נקודה המקיימת |  |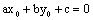
נראה שכל הנקודות המקיימות |
 |
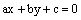יתנו צורה פרמטרית של הישר |
 |
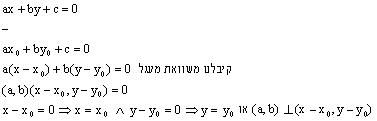| טענה- אם |  |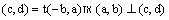
| הוכחה: נתון |  |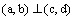
ולכן מתקיים: |
 |
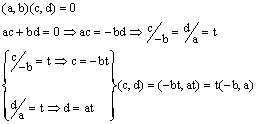גולשים מקוונים: 4