תאוצה

לאחר שלמדנו על מהירות ומיקום, ועל היחס ביניהם, יהיה נקל ללמוד על התאוצה.

הגדרת התאוצה היא -

קצב שינוי המהירות.

נשמע מוכר? נכון, היחס בין מהירות למיקום הוא כמו היחס שבין תאוצה למהירות!

גם התאוצה, כמו המהירות, היא וקטור. אף לגביה נדבר קודם כל על גודל התאוצה, ורק אז על כיוונה וייצוגה כוקטור.

התאוצה אומרת לי, בכמה תגדל מהירותו של גוף, אם תאוצתו תישמר קבועה במשך שניה. כמו שאמרנו לגבי מהירות, גם כאן לא חייבת התאוצה להישאר קבועה, אלא אפשר לדבר על תאוצה רגעית. כלומר, אם ניקח שתי נקודות זמן לאורך תנועתו של גוף, בנקודה הראשונה המהירות היא v1 ובשניה v2. נכנה את הפרש המהירויות בין שתי הנקודות Dv = v2 - v1) Dv). פער הזמן בין הזמן בו היה הגוף במהירות v1 לבין הזמן בו היה הגוף במהירות v2 הוא, כמובן, Dt. התאוצה הממוצעת היא:

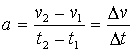
אנו מציינים את התאוצה באות a המורה על המילה האנגלית לתאוצה - acceleration.

כמו שאמרנו קודם, כשדיברנו על היחס בין מהירות למיקום, גם כאן, כאשר נבחר שתי נקודות זמן קרובות מספיק זו לזו, כלומר, כאשר Dt קטן מאד, התאוצה אינה רק הממוצעת, אלא היא התאוצה הרגעית, ברגע הזמן שבין שתי הנקודות.

ראינו שמהירות מודדים במטרים לשניה, כי היא אומרת לנו כמה מטרים מתקדמים כל שניה.

כיוון שהתאוצה אומרת לנו כמו מטרים לשניה של מהירות נוספים כל שניה, מודדים תאוצה במטרים לשניה, לשניה. כך:

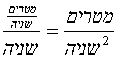
ובקיצור אפשר לומר "מטרים לשניה בריבוע" ולרשום .