- משוואת המשיק

דף ראשי «

מפת האתר «

אודות האתר «

עזרה «

study.eitan.ac.il «

» נושאי לימוד

יום חמישי 25 באפריל 2024

משוואת המשיק

דף ראשי

4 יחידות

חשבון דיפרנציאלי ואינטגראלי

משוואת המשיק

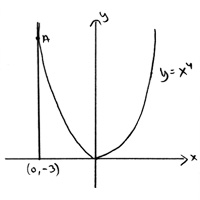
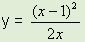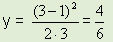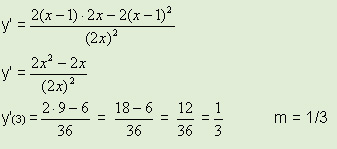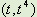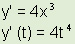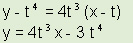משוואת משיק:

בפרק על משוואת קו ישר -אנליטית למדנו שעבור קו ישר יש צורך בנקודה ושיפוע. את השיפוע נקבל באמצאות הנגזרת והצבה של X ולכן קיבלנו 'נוסחה'

(I) y - y1 = m (x - x1)
y - y1 = f '(x1) (x - x1)
שיפוע

מצא את השיפוע בנפרד ועבור לנוסחא I

משוואת משיק לנקודה על גרף הפונקציה:

1.מצא את משוואת המשיק בנקודה x = 3
לפונקציה:

נחשב את ערך y בנקודה

מכאן שהנקודה היא (3,4/6)
נחשב את שיפוע הנקודה:

y – 4 / 6 = 1/3 (x - 3) / * 6
6y - 4 = 2x - 6
6y = 2x - 2

משוואת משיק לנקודה שאינה על גרף הפונקציה:

1. מצא את נקודת ההשקה, ואת משוואת המשיקים לגרף העקומה העוברים דרך נקודה נתונה
שאיננה על גרף הפונקציה.

נקודת ההשקה מסומנת באות A וניתן להסתכל עליה כ -

השיפוע של הישר העובר שם

לכן משוואת הישר תהיה

נותר רק להציב את הנקודה (0,-3)

נציב את t במשוואת המשיק ונקבל:

t = 1 ==> y = 4x - 3
t = -1 ==> y = -4x - 3