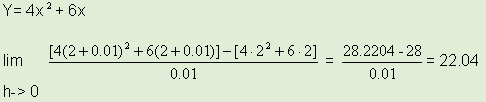| כאשר עסקנו בקווים ישרים ידענו להגדיר את שיפוע הישר ע"י היחס בין הגובה לרוחב, כאשר נעסוק בפונקציות שאינן קו ישר נרצה להתייחס לשיפוע: כאשר שיפוע של פונקציה הינו בעצם שיפוע הישר המשיק לפונקציה באותה נקודה. כלומר השיפוע הוא לא מספר קבוע כי יש לכל פונקציה כמה וכמה משיקים בעלי שיפוע שונה או שווה. לדוגמא L1 , L2 , L3 הם ישרים המשיקים לפונקציה. מהו השיפוע של L3 (אנליטית שיפוע של ישר מקביל לציר ה X) | ||
 | ||
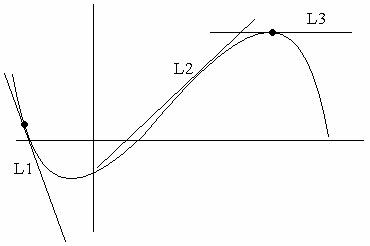ניתן לחשב את השיפוע ע"י חישוב שיפוע על פי שתי נקודות | ||
 | ||
|
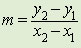פלאש | ||
 | ||
|
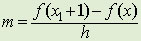דרך זו היא מסורבלת במקום זה עומדת לרשותנו הנגזרת. | ||
|
 |
|||
 |
|
|||
|
יום שבת 20 באפריל 2024
|
|
|
||||||||||||||||||||||||||||||||||
 גולשים מקוונים: 3 |
