מבוא וחוקי קירכהוף
הכרנו בפרקים הקודמים שיטה לפתירת רשתות חשמליות מורכבות הכוללות שתי עניבות, באמצעות חוקי קירכהוף, וכעת נבצע תזכורת קטנה ע"י דוגמא.
את חוקי קירכהוף ניסחנו כדלהלן:
- סכום הזרמים הנכנסים לצומת, שווה לסכום הזרמים היוצא ממנו.
- סכום מפלי המתח במעגל טורי, שווה למתח המקור.
נתבונן בדוגמא הבאה:
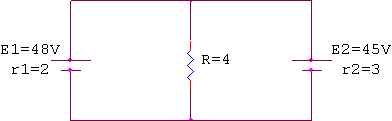
בשלב הראשון יש לקבוע את כיווני הזרמים בכל אחד מהענפים באופן שרירותי לצורך החישובים.
נקבע את כיווני הזרמים כדלהלן:
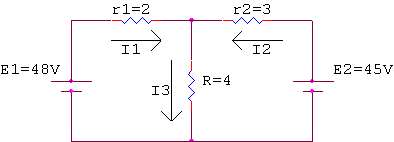
כעת נפנה לחישובים.
על פי חוק הצומת:
I3 = I1 + I2
לפי העניבה הראשונה:
E1 = I1·r1 + I3·R
לפי העניבה השניה:
E2 = I2·r2 + I3·R
נציב נתונים בשתי המשוואות ונקבל:
48 = 2I1 + 4I3
45 = 3I2 + 4I3
נציב במשוואה השניה I2 = I3 - I1 :
48 = 2I1 + 4I3
45 = 3I3 - 3I1 + 4I3
ומכאן נקבל ש:
48 = 2I1 + 4I3
45 = -3I1 + 7I3
נכפול את המשוואה הראשונה ב – 3 ואת המשוואה השניה ב – 2 ונקבל:
144 = 6I1 + 12I3
90 = -6I1 + 14I3
נחבר את המשוואות ונקבל:
234 = 0 + 26I3
ולכן:
I3 = 234 / 26 = 9 A
בשיטה הנ"ל התרנו את הרשת הנתונה לנו באמצעות חוקי קירכהוף, אותם למדנו בפרקים הקודמים.
כעת נעבור לשיטות אחרות להתרת רשתות, שלעיתים הן נוחות יותר ומהירות יותר.
