תרגיל מס' 2
בתרגיל זה נעסוק בנושא הוקטורים, נתרגל פעולות על וקטורים, וקטורים ומשואות לינאריות, מכפלה פנימית, מרחק, זויות והיטלים
פתור את התרגילים וכך תוכל לתרגל נושאים אלו.
בהצלחה!!!
לתרגילים המסומנים ב- תוכל למצוא פתרון מפורט במאגר הפתרונות.
1 ) יהיו u = (2, -7, 1) , v = (-3, 0, 4) , w = (0, 5, -8)
א) מצא את 3u - 4v
ב) מצא את 2u + 3v - 5w
א) 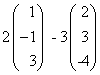 ב)
ב) 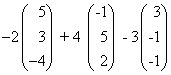
3 ) מצא את x ו- y אם:
א) (x, 3 ) = (2, x + y)
ב) (4, y ) = x(2, 3)
4 ) הפוך את המשוואה הוקטורית הבאה למערכת שקולה של משוואות לינאריות
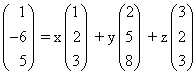
5 ) כתוב את הוקטור v = (1, -2, 5) כקומבינציה ליניארית של הוקטורים
u1 = (1, 1, 1) u2 = (1, 2, 3) u3 = (2, -1, 1)
6 ) כתוב את הוקטור v = (2, 3, -5) כקומבינציה ליניארית של הוקטורים
u1 = (1, 2, -3) u2 = (2, -1, -4) u3 = (1, 7, -5)
7) קבע אם הוקטורים u3 = ( 1, -5, 3) u2 = ( 2, -1, 3) u1 = ( 1, 1,1)
תלויים או בלתי תלויים ליניאריות.
8) קבע אם הוקטורים (3, 2, 1) , (2, 3, -1), (1, -2, -3) תלויים לינארית.
9) נניח ש- w = (1, 6, -7) , v = ( 5, -3, 4), u = (3, 2, 1)
מצא את :
א) ( u + v) ∙ w ב) u ∙ w + v ∙ w
10 ) יהיו u = (5, 4, 1) v = ( 3, -4, 1) w = (1, -2, 3) איזה זוג מהוקטורים
הללו, אם בכלל, הוא של וקטורים ניצבים זה לזה?
11) מצא את |w| אם w = (-3, 1, -2, 4, -5)
12) נרמל w = (4, -2, -3, 8)
13) מצא את המרחק d(u,v) בין הוקטורים u ו- v כאשר:
א) u = (1, 7) , v = (6, -5)
ב) u = (3, -5, 4) , v = (6, 2, -1)
ג) u = ( 5, 2, 1, 0, 8), v = (-4, -3. 1, 3, 9)
14) הוכח כי פונקצית המרחק d (u, v) מקיימת את הדרישות הבאות:
א) d(u, v) ≥ 0 ו- d (u, v) = 0 אם ורק אם u = v.
ב) d(u , v) = d (v, u)
ג) d (u, v) ≤ d (u, w) + d (w, v) (אי – שיוון המשולש )
15 ) מצא את cosα כאשר α היא הזוית בין u = (1, 2, -5) ו- v = (2, 4, 3).
16 ) מצא proj (u , v) כאשר u = (1, -3, 4) ו- v = ( 3, 4, 7)







