שימור התנע

נסתכל במקרה הבא:

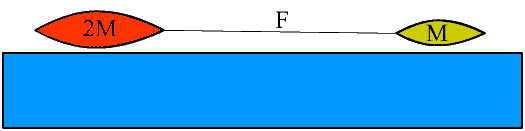
שתי רחפות, רחפת א' במסה של M קילוגרם, ורחפת ב' במסה של 2M קילוגרם.
הרחפות עומדות במקומן. אין חיכוך בין הרחפות למים. הרחפות מרוחקות כמה מאות מטרים זו מזו, וישנו חוט רפוי המחבר ביניהן.
לפתע, נמתח החוט ע"י הימאים שעל סיפון הרחפות. החוט מפעיל כח F על כל רחפת. אנו זוכרים את החוק השלישי של ניוטון ויודעים שבעוד שרחפת א' מרגישה את הכח לכיוון שמאל, רחפת ב' מרגישה אותו לכיוון ימין.
לאחר  שניות מהרגע שנמתח, החוט נקרע. נראה מה מהירות הרחפות מיד לאחר שנקרע החוט-

על רחפת א' פעל כח של F ניוטון, ולפי החוק השני, משמעות הדבר היא שהיא הואצה במשך Dt שניות בתאוצה של . הרחפת השניה כבדה פי 2 ולכן היא הואצה ע"י אותו כח בתאוצה קטנה פי 2 -.
כבר מזמן אנו יודעים שאם גוף הואץ בתאוצה קבועה a במשך זמן t, מהירותו היא a×t. ולכן ניתן לחשב את מהירות רחפת א': 

  ואת מהירות רחפת ב': .

אנו רואים שמהירותה של הרחפת הכבדה יותר קטנה פי 2.
עכשיו נסתכל על התנע- לרחפת הקלה נוסף תנע שמאלה של

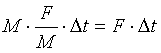
ואילו לרחפת הכבדה נוסף תנע ימינה של

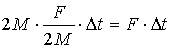
גם כן. (הכפילנו מסות במהירויות). אך כיוון שתנע הוא וקטור, הסכום של תנעים שווים בגודלם והפוכים בכיוונם הוא אפס. וזה גם התנע שהיה בהתחלה, כששתי הרחפות היו במצב נייח.

המשמעות של מה שהראנו עכשיו היא כזו:

התנע בתוך מערכת בה מופעלים כוחות פנימיים בלבד - נשמר!

נפרט את המשפט הנ"ל-

"התנע בתוך מערכת", הכוונה לסכום (וקטורי!) של התנעים של כל הגופים במערכת.

"כוחות פנימיים בלבד", הכוונה לכוחות שפועלים רק בין גופים במערכת.

נסתכל על דוגמה:

כדור מתגלגל על הרצפה עד שנעצר. היה לכדור תנע ולאחר שנעצר התנע שלו התאפס. לאן הלך שאר התנע? התשובה היא שהכדור איננו מערכת סגורה. כח חיכוך פועל עליו מצד הרצפה. ולכן התנע ש"נעלם" הלך לרצפה. ומכיוון שגם הרצפה אינה מערכת סגורה, התנע עבר לכדור הארץ. התנע שהיה קודם רק בכדור, נמצא עכשיו בכדור ובדור הארץ כאחד. אך כיוון שהמסה גדלה מאד (מסת כדור הארץ לעומת מסת הכדור הקטן שעל הרצפה), אין התנע מתבטא בעליית מהירות משמעותית של כדור הארץ.

נזכור עובדה חשובה:

כיוון שתנע הוא וקטור, חוק שימור התנע פועל על כל אחד מרכיבי וקטור התנע. כלומר, במערכת סגורה, סך התנע בכיוון x נשמר וגם סך התנע בכיוון y נשמר וכו'.

לעובדה זו ישנה חשיבות מיוחדת במקרה בו מערכת היא סגורה במחינת כוחות בציר מסויים, ואינה סגורה מבחינת כוחות בצירים האחרים.
למשל, אם אנו יודעים שכוחות חיצוניים פועלים רק בציר ה-y, אין שום סיבה שסך התנע בכיוון x לא יישמר.

נתבונן בסרט המציג מקרה בו מומחשים כמה מהעקרונות הנ"ל: