משתנים כלליים ופרטיים- המשך
ננסה להבין מה קורה בתוככי זיכרון המחשב בהגדרת הנתונים והעברת ערכים לתת-תוכנית.
המחשב בנוי מתאים-תאים, שבחלקם נמצאות הוראות התוכנית ובחלקם המשתנים. לכל משתנה יש כתובת (מספר התא בזיכרון), שכאשר התוכנית או התת-תוכנית פונה לשם שלמשתנה היא בעצם פונה לכתובת.לכן, נראה כיצד בתת-התוכנית מוגדרות כתובות חדשות לכל משתנה שלא הועבר על ידי var.
לצורך ההסבר, נניח שקוראים לתת-תוכנית:
אין זה משנה מהם השמות שהוגדרו בתת-תוכנית. אם הוגדר משתנה, תת התוכנית תכיר רק את השם החדש שהוכר. אם לא, הרי שתת- התוכנית תכיר את המשתנה הכללי.
דוגמא:
כתוב תוכנית הקולטת מספר כלשהו טבעי N (שלם או שווה אפס). מחשבת ומדפיסה אם מספר זה הוא ראשוני.
פתרון:
מספר ראשוני הוא מספר המתחלק, ללא שארית, רק בעצמו וב-1.
נציג שתי אפשרויות לאלגוריתם (יש יותר).
דרך ראשונה: נוודא שהמספר ראשוני על ידי חילוק המספר בכל המספרים עד שורש המספר N (מספר זוגי אינו ראשוני, כמובן).
דרך שניה: נחלק את המספר N בכל המספרים עד 2/N.
בדרך הראשונה, נבצע סך הכל שורש N בדיקות במקרה הגרוע ביותר (שהמספר הוא ראשוני וצריך לבצע את כל הבדיקות) דרך זו מגדילה את היעילות של האלגוריתם על פני האפשרות השניה שבה יבוצעו במקרה הגרוע ביותר 2/N בדיקות.
|
program FIND_DIVIDER; { תוכנית המדפיסה הודעה אם מספר כלשהו טבעי הוא ראשוני } var N: integer; (* בתוכנית הראשית אין עניין במשתנים מקומיים אחרים *)
procedure DIVIDE_ROOT_N (NUMBER:integer); { תת תוכנית המוצאת מחלק של מספר} { N – מקבל את ערכו מ NUMBER } (* כאן נגדיר משתנים שישמשו לצורך פנימי בלבד ללא העברת ערכים *) var ROOT: integer; (* שורש המספר שבודקים את ראשוניותו *) I:integer; (* מונה הלולאה *) FIND_DIVIDER: boolean; (* דגל המציין מציאת המחלק *) begin FIND_DIVIDER:= false; (* עדיין לא נמצא *) ROOT:= trunc(sqrt(NUMBER) + 1); (* השלם הגדול הקרוב לשורש *) I:=3; (* הצבת ערך התחלתי למונה- נתחיל בשלוש *) while ((not FIND_DIVIDER) and (I<=ROOT)) do begin if ((NUMBER mod I) = 0) then FIND_DIVIDER:=true; I:=I+1; (* קדם למספר הבא *) end; if FIND_DIVIDER then writeln (NUMBER,' IS NOT PRIME NUMBER!') end;
procedure INPUT_THE_NUMBER(var INPUT_INT_NUM:integer); { תת תוכנית לקלט } (* var INPUT_INT_NUM – var – המשתנה המועבר מוגדר ב *) (* לאחר סיום תת –התוכנית N כדי ששינוי ערכו ישנה את *) begin write ('Enter a natural number: '); readln (INPUT_INT_NUM); end;
(********* התוכנית הראשית **********)
begin INPUT_THE_NUMBER(N); (* של התוכנית var הוא משתנה שהוגדר ב N *) if ((N mod 2 ) <> 0) then DIVIDE_ROOT_N(N) else writeln (N,' is not prime because he is even!'); end.
|
![]() להורדת הדוגמא לחץ כאן
להורדת הדוגמא לחץ כאן
דוגמת ריצה:
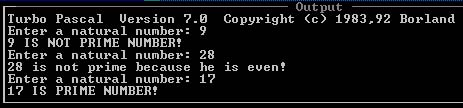
בדוגמא זו נשים לב לייחודיות של תת התוכנית N_ROOT_DIVIDE על כל משתניה המקומיים. NUMBER הוא משתנה מקומי הנעלם בסיום התת-תוכנית. הוא הוגדר מיד לאחר הגדרת שם התת-תוכנית כי למשתנה זה מעבירים ערך עם תחילת הביצוע של תת התוכנית.
יעילות האלגוריתם
בדוגמא הקודמת הזכרנו נושא חשוב מאוד העוסק ביעילות האלגוריתם.
בדרך כלל בפיתוח אלגוריתמים ענייננו יהיה, כמה זיכרון (תאי זיכרון) וכמה זמן ידרוש יישום האלגוריתם במקרה בו יידרשו לפתרון הבעיה מירב הצעדים.
לכך יש חשיבות גדולה מאוד כאשר באים ליישם את האלגוריתם במחשב באמצעות שפת תכנות. כך נוכל להעריך אם הפתרון מתאים לצרכינו.
לדוגמא,אלגוריתם שלצורך הפלט יבצע מספר צעדים גדול מאוד, כך שמחשב בן זמננו יבצע אותו באלפי שנים, אינו בר-יישום. או אלגוריתם שלצורך ביצועו יידרשו מספר תאי הזיכרון הגדול ממספר האטומים ביקום גם הוא בר-ביצוע.
כיצד נספור או כיצד נמצא כמה יעיל מבחינת זמן אלגוריתם אחד ממשנהו (לפתרון אותה בעיה כמובן)?
נמדוד זאת על ידי חישוב הזמן שצריך ביצוע אלגוריתם זה לרוץ לעומת הזמן שצורכת ריצת האלגוריתם האחר במקרה הגרוע ביותר. במילים אחרות, ריצה הצורכת את הזמן המקסימלי עד לפתרון באלגוריתם זה, לעומת האלגוריתם האחר.
לדוגמא,כאשר נציע שני אלגוריתמים המדריכים תלמיד לכיתתו בקומה העשירית: לך ישר,עלה במדרגות או במעלית אם היא פנויה (בדרך כלל היא תפוסה...), יעילותו שלהאלגוריתם הטוב ביותר מביאה בחשבון שלצורך הגעת התלמיד בכיתה יש לבצע את מירב הצעדים (ולא במקרה המיוחד שהמעלית פנויה).
|
כמות הזמן בביצוע אלגוריתם, משתקפת במספר הצעדים (או פעולות היסוד-הוראות) שעל האלגוריתם לבצע במקרה שבו יידרשו מירב הצעדים לפתרון. |
כתוב תת תוכנית הקולטת מספר טבעי N (שלם וחיובי) ומדפיסה את עצרת המספר N.
פתרון:
|
· · קטע הבא לפני תת תוכנית זו · procedure FACTORIAL(N:integer); var P, I: integer; begin P:=1; I:=1; while I<=N do begin P:=P*I; I:=I+1; end; writeln(N, '!=' , P); end; · · קטע הבא אחרי תת תוכנית זו ·
|
![]() להורדת הפרוצדורה לחץ כאן
להורדת הפרוצדורה לחץ כאן
מספר הצעדים עד לפתרון, גדל עם הגדלת המספר N בקלט לתת תוכנית. מספר הצעדים הגדל עם הקלט נמצא בתוך הלולאה (שתי הוראות בלולאה).
לכן, מספר הצעדים לפתרון בתוך לולאה הוא N2. הפתרון הוא מסדר גודל של N.זאת מכיוון שיכול להיות שהאלגוריתם יושם על ידי שפת תכנות אחרת, כך שבתוך הלולאה תהיה פעולת יסוד אחת. אך תמיד באלגוריתם המוצע, תתבצע הלולאה N פעמים.
שימו לב, התעלמנו לחלוטין ממספר הצעדים שאינו גדל עם הקלט (ההוראות מחוץ ללולאה,
;I:=1; P:=1 ), מהם שני צעדים לעומת מאה מיליון לדוגמא. באופן כללי, אלגוריתמים מנותקים מהשפה בה הם מיושמים.
חישוב סדר הגודל של צעדי האלגוריתם מטעה לעיתים כיוון שהוא אינו מביא בחשבון פעולות יסוד המיושמות על ידי שפה מסוימת. לכן, חישוב הזמן של תוכנית (ולא אלגוריתם), ייעשה תוך כדי התחשבות בכל פעולה ופעולה ובשיעור הזמן שפעולה זו דורשת.
