מרכז מסה
נתבונן בשני גופים שמסותיהם m1 ו-m2. לכל אחד מהגופים מיקום (על משטח דו מימדי) שמוגדר על ידי קורדינטות x1 ו-y1 (עבור m1) ו- x2 ו-y2 (עבור m2). נגדיר מיקום X ו-Y בצורה המוזרה הזאת:
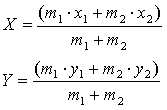
משמעות המשוואות הנ"ל היא- קחו את מיקומו של הגוף הראשון כפול מסתו, הוסיפו למיקומו של השני כפול מסתו, וחלקו את כל מה שקיבלתם בסך המסה של שני הגופים.
הערה: זה חישוב דומה לחישובים של ממוצע. למשל- חישוב ממוצע ציונים בכיתה כאשר ישנן רק 2 אפשרויות לציון או 100 או 50. יש לסכום את כל הציונים שקיבלו כל ילדי הכיתה ולחלק במספר הילדים בכיתה. וכיוון שאפשר לקבל רק 50 או 100, ניתן לסכום את כל ציוני הכיתה ע"י הכפלה של הציון 100 במספר הילדים שקיבלו אותו, ולהוסיף את מכפלת הציון 50 במספר הילדים שקיבלו אותו. ואת התוצאה לחלק במספר הילדים בכיתה. באופן דומה ניתן לומר שמרכז המסה עונה על השאלה "איפה בממוצע נמצאים שני הגופים"
המשוואות שלעיל הן הגדרת המיקום של מרכז המסה.
חשוב לזכור שממשוואות אלה נובע שמרכז המסה קרוב יותר לגוף המאסיבי יותר!
מתוך הגדרה זו של המיקום ניתן גם להגדיר את מהירות מרכז המסה:
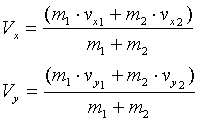
אם נגדיר:
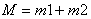
ונכפיל ב-M, נקבל:
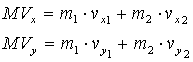
החלק שמימין הוא סכום התנע של גוף 1 וגוף 2. ניתן לראות שאם לוקחים את מהירות מרכז המסה ברכיב כלשהו, ומכפילים במסה הכוללת, מקבלים תנע שהוא בעצם סך התנע של שני הגופים באותו רכיב.
ניתן להגדיר בצורה דומה מרכז מסה עבור כמה גופים שאנו רק רוצים, אך נסתפק בשני גופים כדי להסביר את העניין.
כבר אמרנו שאם המערכת סגורה, אזי התנע של כל גוף בה בנפרד יכול להשתנות, אך סך התנע תמיד נשמר קבוע. כיוון שעכשיו ראינו שה"תנע" של מרכז המסה (דהיינו, מהירותו כפול סכום המסה של כל הגופים) הוא סכום התנע הכללי במערכת, משמעות הדבר היא עובדה חשובה מאד:
במערכת סגורה, נשמר התנע של מרכז המסה.
מכיוון שסכום המסות נשאר קבוע, ניתן לנסח את האמירה הנ"ל גם באופן כזה:
במערכת סגורה, מהירות מרכז המסה אינה משתנה לא בגודלה ולא בכיוונה
נסתכל על דוגמה לנושא:
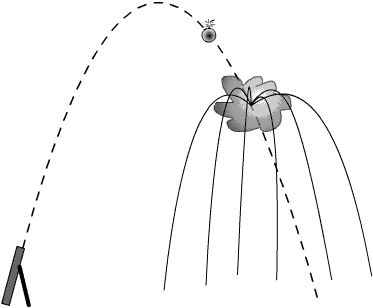
מרגמה יורה פגז, המתפוצץ בשמים. חלקי הפגז נפוצים לכל עבר, אך כיוון שעל כל חלקי הפגז הנושרים למטה פועל כח הכבידה בדיוק כמו שהיה לפי פיצוץ הפגז, מרכז המסה של כל רסיס הפגז ממשיך בתנועה למטה כפי שהיינו מצפים אילו לא היה הפגז מתפוצץ כלל.
התנגשויות
למרכז המסה ישנה חשיבות מיוחדת בהתנגשויות.
ניתן לחלק בין שני סוגים של התנגשויות- התנגשויות פלסטיות והתנגשויות אלסטיות.
בהתנגשות פלסטית, הולך לאיבוד חלק מהאנרגיה הקינטית של הגופים המתנגשים. למשל, אם הגופים הם כדורים רכים, בהתנגשות הם מפעילים כח לאורך דרך בכך שהם מעוותים את צורתם. זו עבודה המשתחררת כאנרגיית חום והולכת לאיבוד. בהתנגשויות כאלה נשמר רק התנע.
בהתנגשות אלסטית לחלוטין, אין שום שינוי צורה ולא הולכת לאיבוד שום אנרגיה. ולכן בהתנגשויות כאלה יש גם שימור של התנע וגם שימור של האנרגיה של הגופים המתנגשים.
כיוון שהתנע של מרכז המסה נשמר, אם נציין את מיקומו במהלך ההתנגשות נראה שמהירותו אינה משתנה כתוצאה מההתנגשות, לא בגודלה ולא בכיוונה
נסתכל בסרט העוסק בהתנגשויות, ומדגים את משמעות מרכז המסה:
