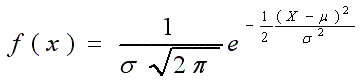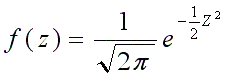|
ההתפלגות הנורמלית הינה החשובה שבהתפלגויות הסטטיסטיות, ואחת הסיבות לכך היא שהתפלגות זאת משמשת קירוב מצוין לקבוצה גדולה של התפלגויות סטטיסטיות, שחשיבותן המעשית רבה (לדוגמא: כפי שניתן לראות בהמשך, ההתפלגות הבינומית וההתפלגות הפואסונית).
התפלגות זאת נקראת גם התפלגות גאוס, על שם המתמטיקאי גאוס שמצאה לראשונה, והשם "נורמלית" מקורו בעובדה שהתפלגות זאת, עקב תכונותיה האופייניות, מתארת בדיוק רב יחסית את התפלגותם של משתנים מקיים של אוכלוסיות רבות ומגוונות, כגון: התפלגות הגובה והמשקל בקרב אוכלוסיית הבוגרים, התפלגות ציונים בכתה, התפלגות הטמפרטורה בתהליך כימי, התפלגות ציוני האינטלגנציה באוכלוסיה ועוד. ההתפלגות מוגדרת ע"י המשוואה:
|
|
|
|
כאשר:
|
|
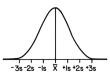
סך כל השטח המוגבל על-ידי העקומה וציר ה-x הוא 1, לכן השטח שמתחת לעקומה והנמצא בין שתי אורדינטות X=a ו- X=b, באשר a<b, מייצג את ההסתברות ש- X נמצא בין a ל- b וסימונה של ההסתברות הזו P(a<X<b). כאשר מבטאים את X במונחים של יחידות תקן,
|
|
במקרה כזה נאמר כי ל- z יש התפלגות נורמלית סטנדרטית (עם ממוצע אפס ושונות אחד).
|
|
|
|
הגובה הממוצע של 500 תלמידים בבית-ספר הוא 151 ס"מ וסטיית התקן היא 15 ס"מ. אם נניח שהתפלגות הגבהים היא נורמלית, מצא כמה תלמידים גובהם: א. פחות מ- 128 ס"מ. ב. 128 ס"מ.
א. סטודנטים שגבהם קטן מ- 128 ס"מ, גובהם קטן מ- 127.5 ס"מ. 127.5 ס"מ ביחידות תקן הם: /15 = -1.57(127.5-151) החלק המבוקש מאוכלוסית התלמידים שווה לשטח שמשמאל ל- z = -1.57 .
שטח זה שווה לשטח שמשמאל ל- z = 0 מינוס השטח שבין z = -1.57 ו- z = 0, כלומר:
0.5-0.4418 = 0.0582
לכן מספר התלמידים שגובהם קטן מ- 128 ס"מ הוא:
500(0.0582) = 29 .
ב. תלמידים שגובהם נרשם כ- 128 ס"מ, גובהם בין 127.5 ס"מ ל- 128.5. 127.5 ס"מ ביחידות תקן הם: (127.5-151)/15 = -1.57
128.5 ס"מ ביחידות תקן הם: (128.5-151)/15 = -1.5
החלק המבוקש מאוכלוסית התלמידים שווה לשטח שבין z = -1.57 ו- z = -1.5 .
שטח זה שווה לשטח שבין z = -1.57 ו- z = 0 מינוס השטח שבין z = -1.5 ו- z = 0 , כלומר:
0.4418-0.4332 = 0.0086.
מספר התלמידים שגובהם 128 ס"מ הוא: 500(0.0086) = 4 |
|
 |
||
 |
|
||
|
יום שישי 22 בנובמבר 2024
|
|
|
|||||||||||||||||||||||||||||||||||
 גולשים מקוונים: 3 |
,
