| פונקציה ריבועית | 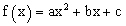 |
הדרכה לשרטוט הפונקציה:
1.
| מציאת נקודות חיתוך עם ציר x | 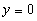 |
| מציאת נקודות חיתוך עם ציר y | 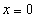 |
2. מציאת נקודות קיצון:
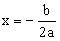 |
קיצון. |
| y קיצון מחשבים ע"י הצבת x קיצון בפונקציה או ניתן למצוא x קיצון ע"י | 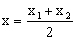 |
קיצון |
| כאשר | 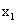 |
ו- | 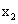 |
הן נקודות החיתוך עם ציר ה-x , מציאת y קיצון ע"י הצבת x קיצון בפונקציה |
המקורית. נקודת הקיצון נקבעת בהתאם ל-a.
| אם | 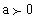 |
הפרבולה מחייכת ולכן נקודת מינימום, עבור | 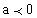 |
הפרבולה בוכה ולכן נקודת |
מקסימום.
3. שרטוט הפונקציה:
| דוגמה: | 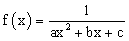 |
שלבים:
| 1. נקודות החיתוך של הפונקציה | 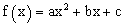 |
עם ציר ה-x הן האסימפטוטות |
| בפונק' זו, כיון שבנקודות אילו | 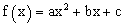 |
מתאפס. ואז המכנה הוא 0 ומקבלים |
ביטוי חסר משמעות (בח"מ).
| 2. נתבונן בתחומי העליה והירידה בפונקציה | 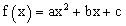 |
| כאשר הפונק' | 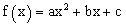 |
עולה, הפונק' | 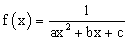 |
יורדת. |
| כאשר הפונק' | 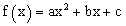 |
יורדת, הפונק' | 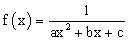 |
עולה. |
| אם יש נק' חיתוך בין הפונק', הנק' יהיו ב- | 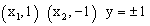 |
| אם נק' החיתוך של | 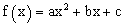 |
עם ציר ה-y היא בנק' | 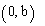 |
| אז נק' החיתוך של | 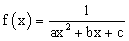 |
עם ציר ה-y היא בנק' | 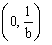 |
פלאש.

