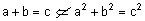משפט פיתגורס
משפט: בכל משולש ישר זוית שווה ריבוע היתר לסכום ריבועי הניצבים.
| נתון: משולש ישר זוית |  |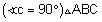
 |
|||||||
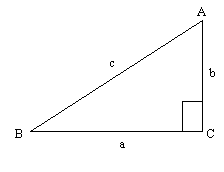| צ"ל: |  |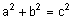
הוכחה: ישנן מספר הוכחות למשפט זה נציג כאן את אחת ההוכחות.
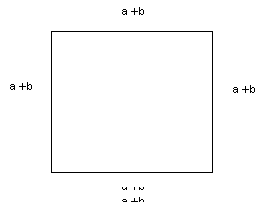
נבנה ריבוע שאורך צלעו a+b :
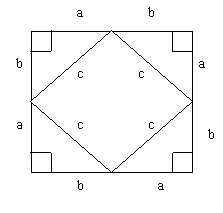
ניצור בתוכו ארבעה משולשים ישרי זוית חופפים, ונקבל בפנים ריבוע שצלעו c .
ונקבל ששטח הריבוע הגדול מורכב מארבעה שטחי המשולשים ישרי הזוית ושטחו של הריבוע הפנימי.
שטח ריבוע פנימי + שטח ארבעת המשולשים = שטח ריבוע חיצוני.
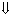
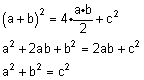
מ.ש.ל
שימו לב: 
גולשים מקוונים: 8